四角形の面積(「ヘロンの公式」応用) 作者 darkn さん 実行数 5152 一対の対角(の和)が判っていれば,ブレートシュナイダーの公式(Bretschneider's formula) が使えますが,ここでは「長さ情報」のみを使用しています. 辺ABの長さ · Excelで、ヘロンの公式により三角形の面積を求める方法(三角形の三辺の長さから、その三角形の面積を求める)についてです。 LET関数を使うことで、比較的短い式でヘロンの公式を記述して三角形の面積を求めることができます。手順 画像ではC2,C3,C4セルに三角形の辺a,b,cの長さが入力されて · 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。

この問題なんで Ahbや Abhに着目して考えるのか分かりません 解説お願いし Clear
ヘロンの公式 四角形 面積
ヘロンの公式 四角形 面積-ヘロンの公式を使わない場合は、 1 余弦定理でひとつの角の$\cos$を得る 2 $\sin^{2}\theta\cos^{2}\theta=1$を用いて、その角の$\sin$を得る 3 復習の2番目の公式を使って面積を求める という手順になる。 余弦定理より、ヘロンの公式再考 宇佐美 広介 岐阜大学工学部 要旨 ヘロン( Heron )の公式とは三角形の面積をその3 辺の長さのみを用いて書き表す公式で あり,古来より著名なものである.しかも,その表示式は美しい対称性・構造を持ってい
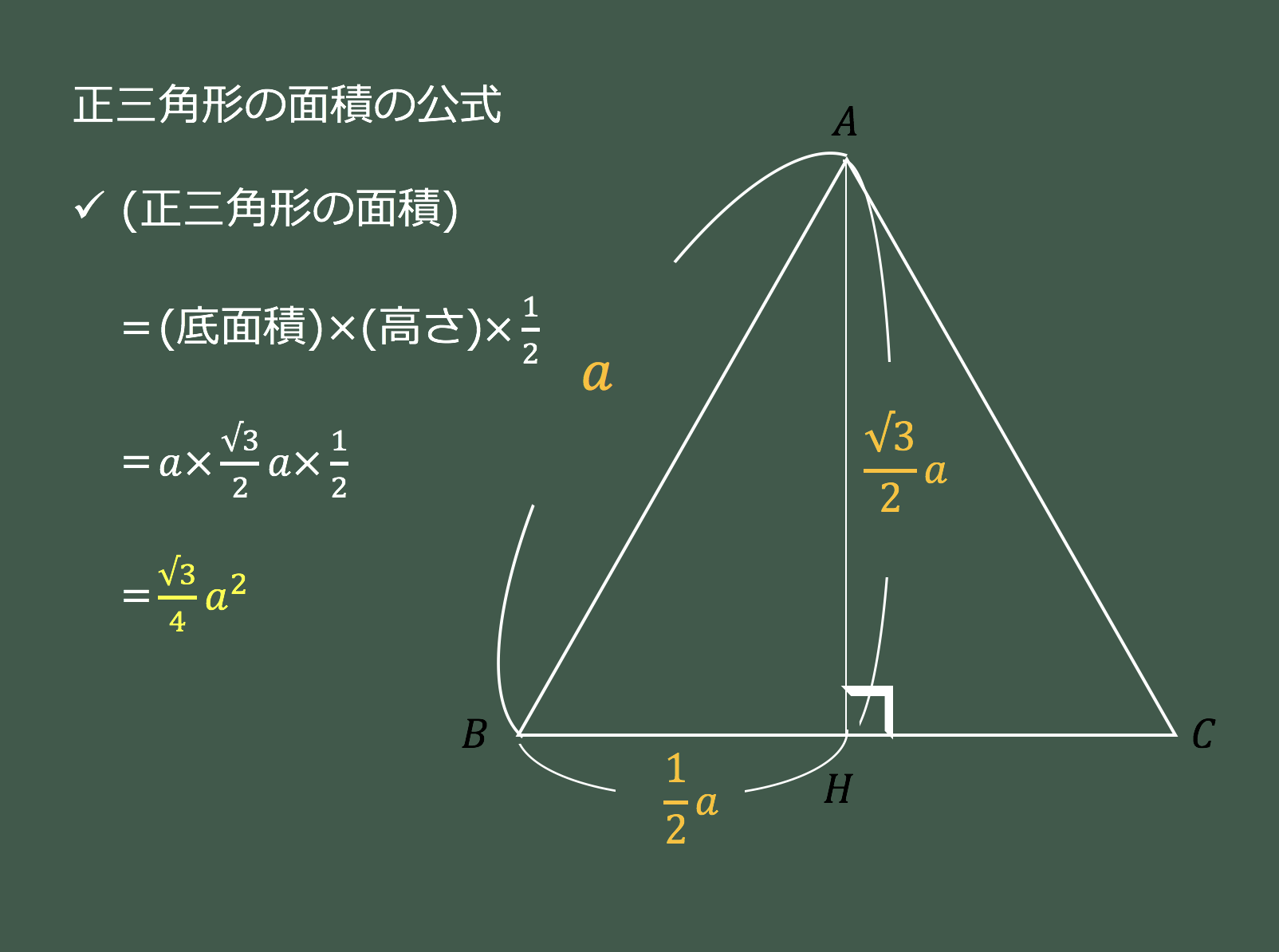



最高 50 正三角形 面積 求め方
円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円ブラマグプタに大いに感謝しなければならない。 ブラマグプタの公式 円に内接する四角形の4辺の長さを、a、b、c、d とするとき、 四角形の面積 S は、 で与えられる。 (証明) S= ABC+ ACD において、B+D=180°より、sinB=sin D なので、 2S=(ab+cd)sin B ここで、余弦定理により、AC2=a2+b2-2abcos B=c2+d2-2cdcos D B+D=180°より、cos D=-cos B であることに注(1) で示した等式は「ヘロンの公式」(Heron's formula)と呼ばれる $3$ 辺の長さと面積が整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼び, そのうち $3$ 辺の長さが連続する整数であるものを「ブラーマグプタの三角形」(Brahmagupta triangle)と呼ぶ 本問の結果により,「ブラーマグプタの三角形」の $2$ 番目に長い辺の長さ $b$ と「ペル方程式」$x^23y^2 = 1$ の解は
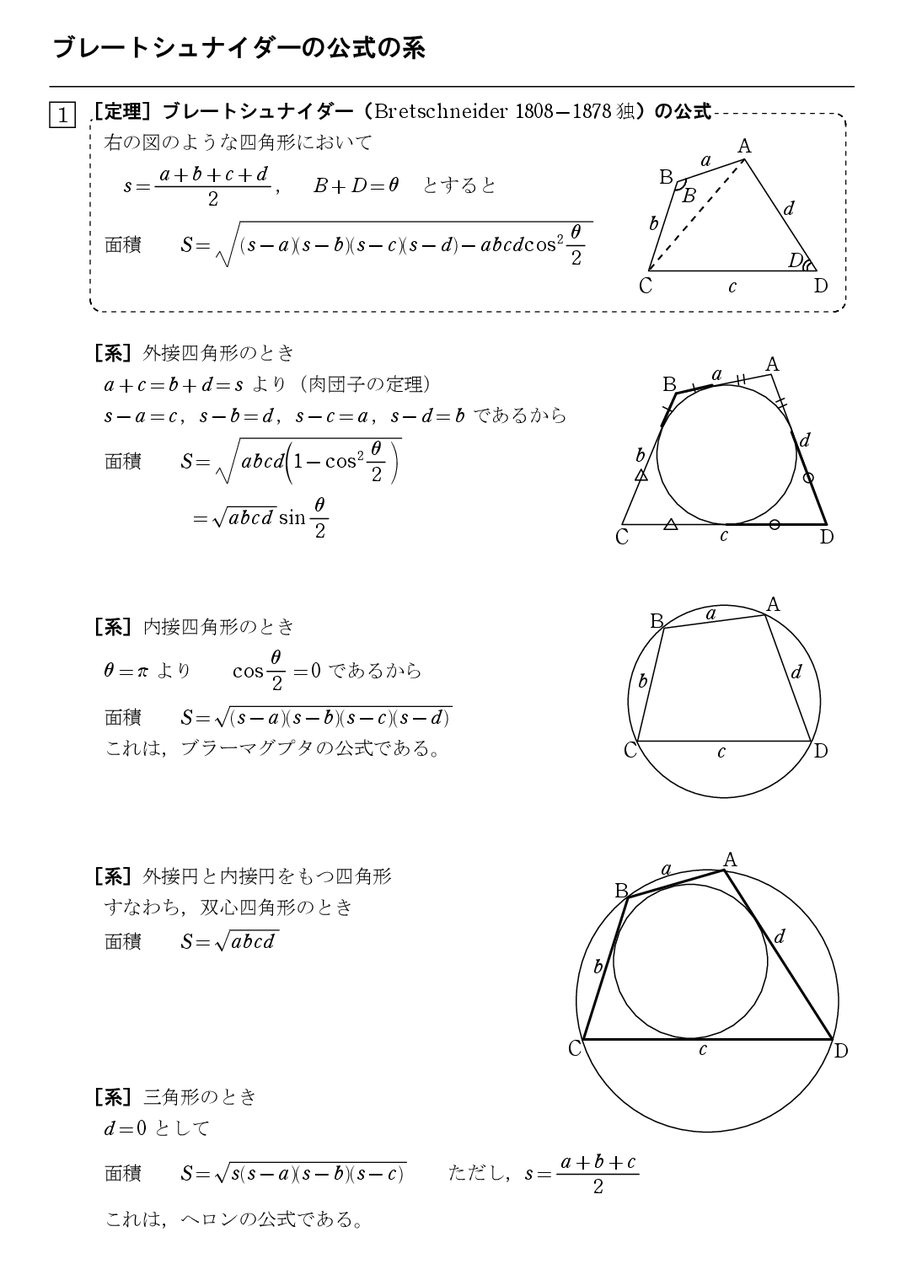
Page 5 この公式において,辺の長さd を限りなく0に近づけると四角形は三角形となりヘロンの公式を得る. 四角形の面積公式から眺めると,s は「周の長さの半分」と捉える方が自然といえるのである. ブラマグプタ(598~660)は,アリヤバータ(476~550)とともにグブタ王朝時代のインドを代表す · 三角形の面積の公式 三角形の面積には、いくつかの求め方があります。 ここでは、代表的な三角形の面積の公式 \(3\) つを紹介します。 公式①底辺 × 高さ ÷ 2 まず \(1\) つ目は、底辺と高さを使った最もオーソドックスな公式です。 · 四角形の面積にまつわる公式 ブラーマグプタの公式とその証明 円に内接する四角形の面積をヘロンと同じノリで求める有名な公式です。 ブレートシュナイダーの公式 ブラーマグプタの公式の一般化です。これはあくまで観賞用ですかね。
するとヘロンの公式から三角形の面積 S は、 根号内のカッコの中を y とおくと、 なので、 x = 0 、 a で y '= 0 となります。 x = a を S の式に代入すると、 となります。 これは、 1 辺が a の正三角形の面積 · ヘロンの公式による三角形の面積の計算を確定させると以下の通りとなります。 このようにしてエクセルにてヘロンの公式から三角形の面積を計算できるのです。 今回の場合は約342mm3となるといえます。このとき、単位を付け直すことを忘れないようにしてください。なお、単位を含めた数値 · これでヘロンの公式を表すheron関数を定義できました。 辺の長さがそれぞれ3, 4, 5の三角形の面積を求めてみましょう。 heron( 3, 4, 5 ) # 60 この三角形は直角三角形で面積は3×4÷2=6となり、この関数の計算が正しいことが確認できました。
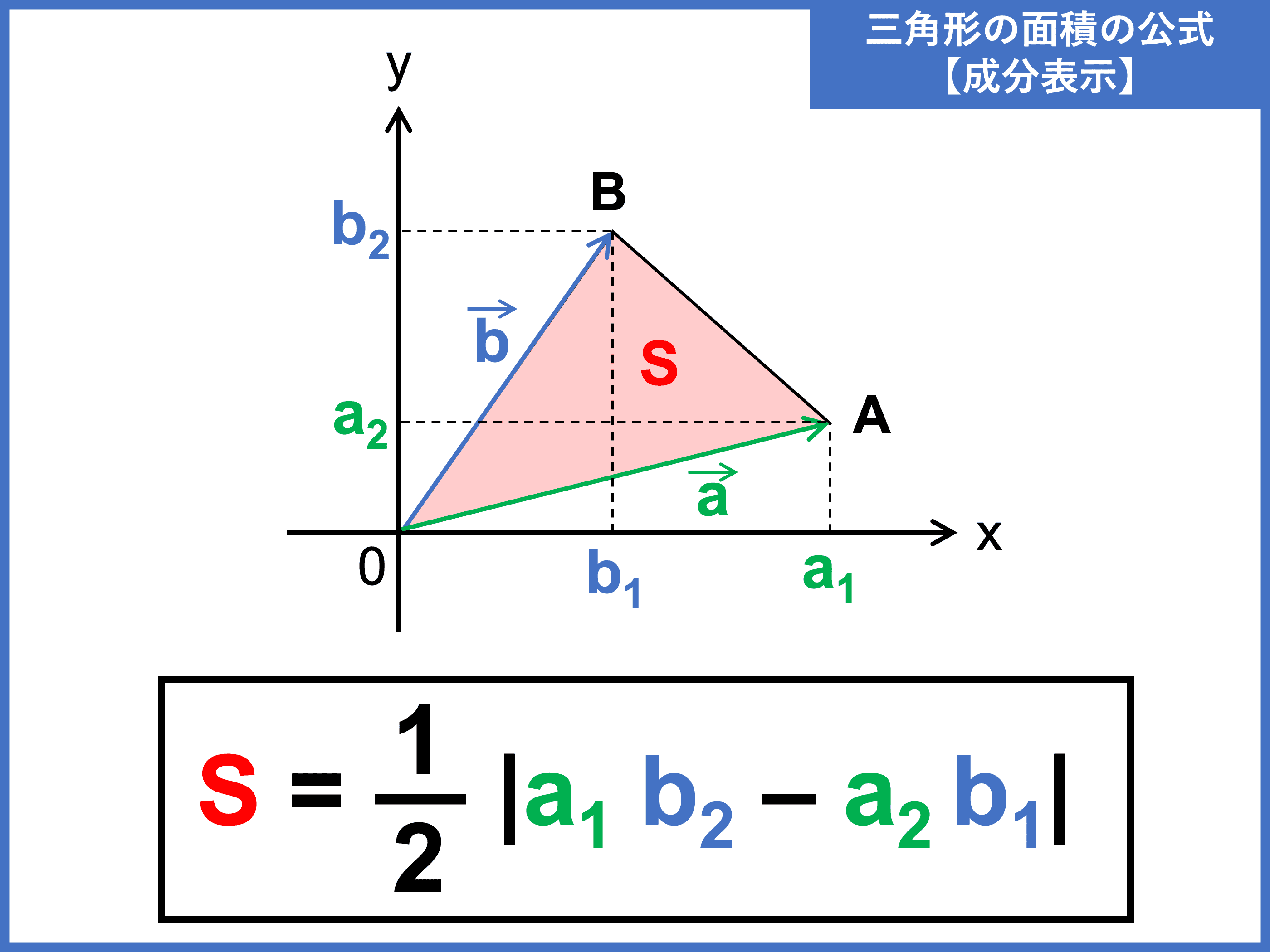



三角関数 面積 公式 証明




正方形の中にある三角形の面積の平均 Musyokutoumei
ヘロンの公式(ヘロンのこうしき、英 Heron's formula )とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。 アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる 。 目次 1 概要 · ヘロンの公式 AB = c A B = c, BC = a B C = a, CA = b C A = b と書き、角の大きさは ∠CAB = A ∠ C A B = A, ∠ABC = B ∠ A B C = B, ∠BCA = C ∠ B C A = C と書くことにします。 標準三角比と三角形の面積 の例題のように、 a,b,c a, b, c がわかっているときに、この三角形の面積三角形の面積を求める関数の定義 3つの三角形A,B,Cがある。それぞれの三角形の3辺の長さは, Aが12,15,9,Bが22,12,16,Cが31,32,9である。 ヘロンの公式を用いて, 三角形の面積を返す関数を定義しなさい。ここで,引数は3辺の長さとし, 3辺の長さを3つの整数型の変数で与える場




円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張
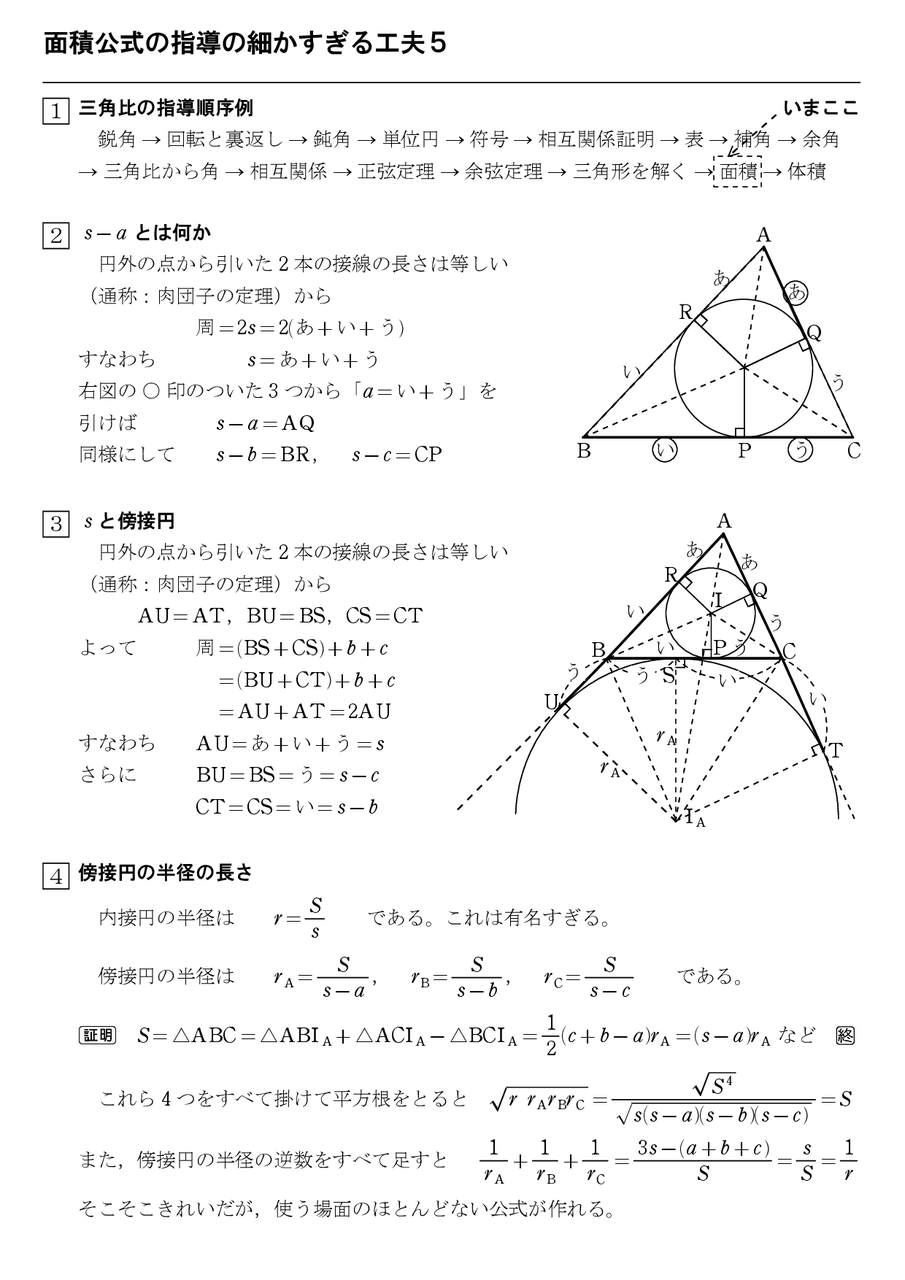



15年08月 怜悧玲瓏 高校数学を天空から俯瞰する
ABCの面積は ですが、ahをa,b,cだけの式に直すと、ヘロンの公式となります。 図で、h 2 =c 2 x 2 =b 2 (ax) 2 、従って c 2 x 2 =b 2 a 2 2axx 2 から となります。ヘロンの公式とは、三角形の三辺の長さのみの情報からその面積を計算できる式のことを指します。 具体的には、 s=1/2(abc)とした場合に、面積S=(s(sa)(sb)(sc))^05 で表すことができる計算式がヘロンの公式です。三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




数学も英語も強くなる 意外な数学英語 Unexpected Math English December 18
· ヘロンの公式と同じ理由ですか?教えてください(_ _) 数学 円に内接する四角形abcdにおいて、ab=3、bc=2√2、cd=1、da=√2であるとき、 (1)∠b (2)四角形abcdの面積 この問題がわかりません、教えてください 数学 四角形abcdは正方形、三角形ebcが正三角形の時、どうしてeb=ab、ec=dcだと分かるんですか三角形の面積の公式 三角形の面積の公式といえば、 (底辺)×(高さ)÷2 で、お馴染みである。 基本的に、面 積の公式は全て、この公式が出発点である。 例1.の変形バージョンとしては次の公式が有名だろう。 ただし、sは、三角形の周の長さの半分 · 四角形の4つの辺の長さ a, b, c, d に加え、どちらか一方の対角線の長さ e が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 S 1, S 2 を ヘロンの公式 を使って求め、それらを合計することで四角形の面積を求めることができます。




この問題なんで Ahbや Abhに着目して考えるのか分かりません 解説お願いし Clear




三角比 Hashtag Videos On Tiktok
· 四角形を \(2\) つの三角形に分けて 、三角形の面積の公式「\(\displaystyle S = \frac{1}{2} bc \sin \mathrm{A}\)」で面積を表します。 ヘロンの公式の証明と同様、三角比の相互関係と余弦定理を用いて三角比を辺の長さで表現すれば証明できます。 · 今回は、ヘロンの公式を用いて三角形の面積を求めるためのサンプルプログラムを作成したので紹介したいと思います。 コードは、下記のようになります。 import math print("三角形の3本の辺の長さを入力してください。\n") print('a=') a=float(input()) print('b=') b=floatS S S が整数であるような三角形を ヘロンの三角形 (Heronian triangle)と呼ぶ また, ヘロンの三角形の 3 3 3 辺の長さの組 ( a, b, c) (a,b,c) (a,b,c) を ヘロン数 (Heronian number)と呼ぶ ヘロンの公式により, これは S = 1 4 ( a b c) ( − a b c) ( a




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
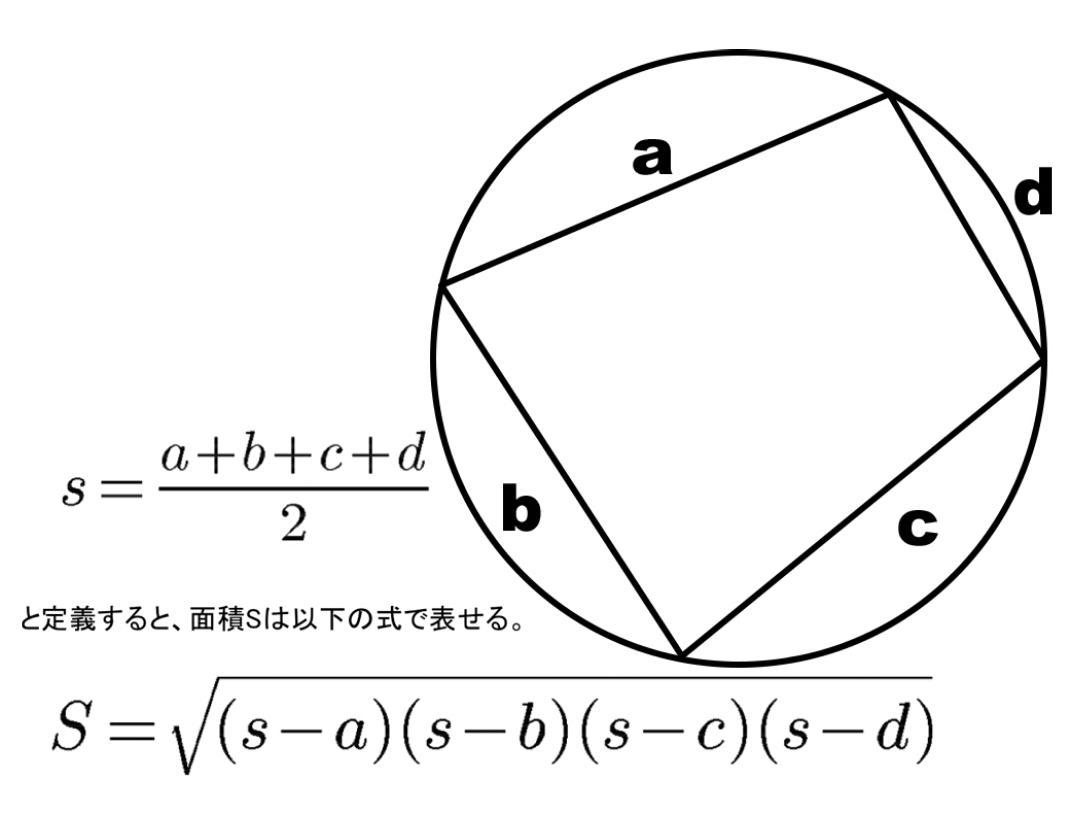



どちゃ楽数学bot ブラーマグプタの公式 ブレードシュナイダーの公式で8 Pの場合 つまり円に内接する四角形の面積 Sを求める公式 検算用 T Co Lprfy7g2
正三角形では3内角の大きさは等しく,60度であるが,逆に3内角の大きさが等しい三角形は正三角形となる (図5)。 三角形の面積 S は, S =1/2 ah ,または (ヘロンの公式)で与えられる。ヘロンの公式 3辺の長さが \ (a\) \ (b\) \ (c\) の三角形 \ (ABC\) の面積 \ (S\) は $$S = \sqrt {s (sa) (sb) (sc)}$$ で計算することができます。 ただし $$s = \frac {abc} {2}$$ です。2 四角形の面積の求め方 4 √ s(s a)(s b)(s c) ただし, s = abc 2 (6) 2 四角形の面積の求め方 頂点をA;B;C;D とし, AB = p;BC = q;CD = r;DA = s とする 21 ブレートシュナイダーの公式 三角形の求積方法にヘロンの公式(6) が存在するように, 各辺の長さと対角の大きさから四角形の面積S を
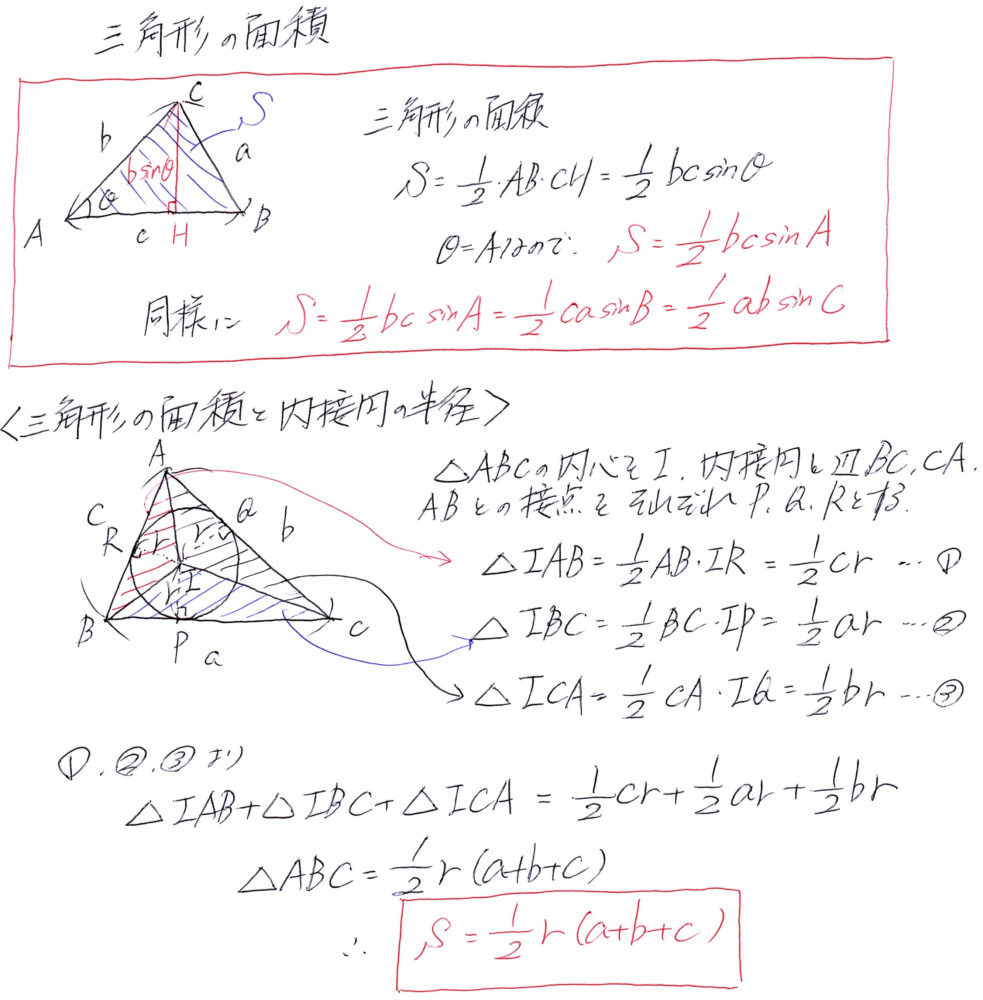



三角形の面積と形状 富岡市の総合学習塾 トータルアカデミー




高校数学 数 93 三角形の面積 基本編 Youtube
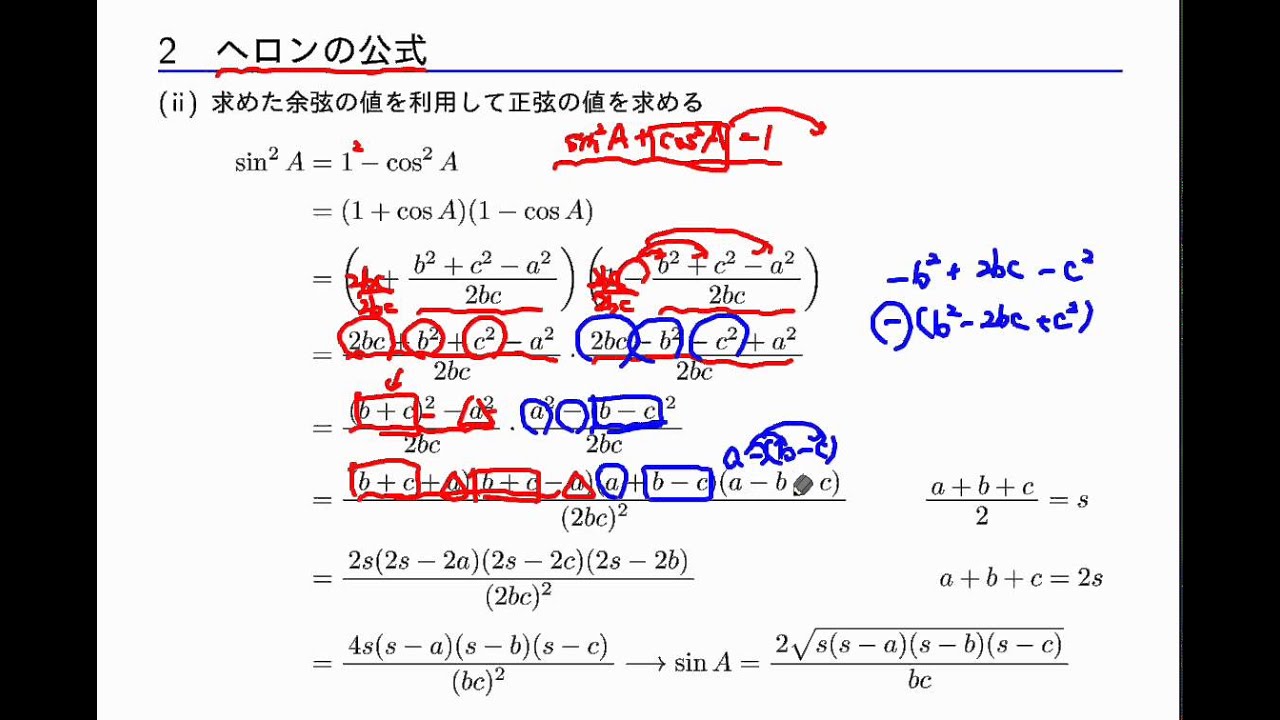
· また、最後はヘロンの公式がどうして成り立つのかを丁寧な式変形によって、解説していきたいと思います。 ヘロンの公式とは どんなときに使えるの? 三角形の面積を求めるための公式はたくさんあります。 その中でも「ヘロンの公式」というものがあります。以下のような公式ですね。 $$\text{三角形の面積\(S\)} = \sqrt{s(sa)(sb)(sc)}, \qquad s=\frac{abc}{2}$$ \(a\), \(b4点の座標から四角形の面積を計算する方法の考え方を知りたいと思います。 測量では三斜法と言うようです。どうやら、この方法は、三角形以上の凸多角形の面積が計算できそうです。 4点 a,b,c,d が上の図のような配置だとします。上の左図の3つの台形の面積の和から、上の右図の台形の面積ヘロンの公式 三角形の面積を求めるときに用いたヘロンの公式を紹介します。 <証明> 使用する公式 ・三角関数の基本公式 sin 2 Acos 2 A=1 ・余弦定理 a 2 =b 2 c 22bccosA b 2 =c 2 a 22cacosB c 2 =a 2 b 22abcosC ・三角形の面積の公式(面積をSとする) S= 余弦定理の第1式より cosA= (1) sin 2 Acos 2 A=1




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




ヘロンの公式 計算を工夫して証明 今週の定理 公式no 4 Youtube
ヘロンの公式 の用例・例文集 円の内接四角形の面積を求めるその式は、ヘロンの公式を内包している。ヘロンの公式はこれらの公式の特別な場合となっている。これは三角形におけるヘロンの公式を一般化したものである。これは三角形の面積を辺の長さで表すヘロンの公式と面積公式を
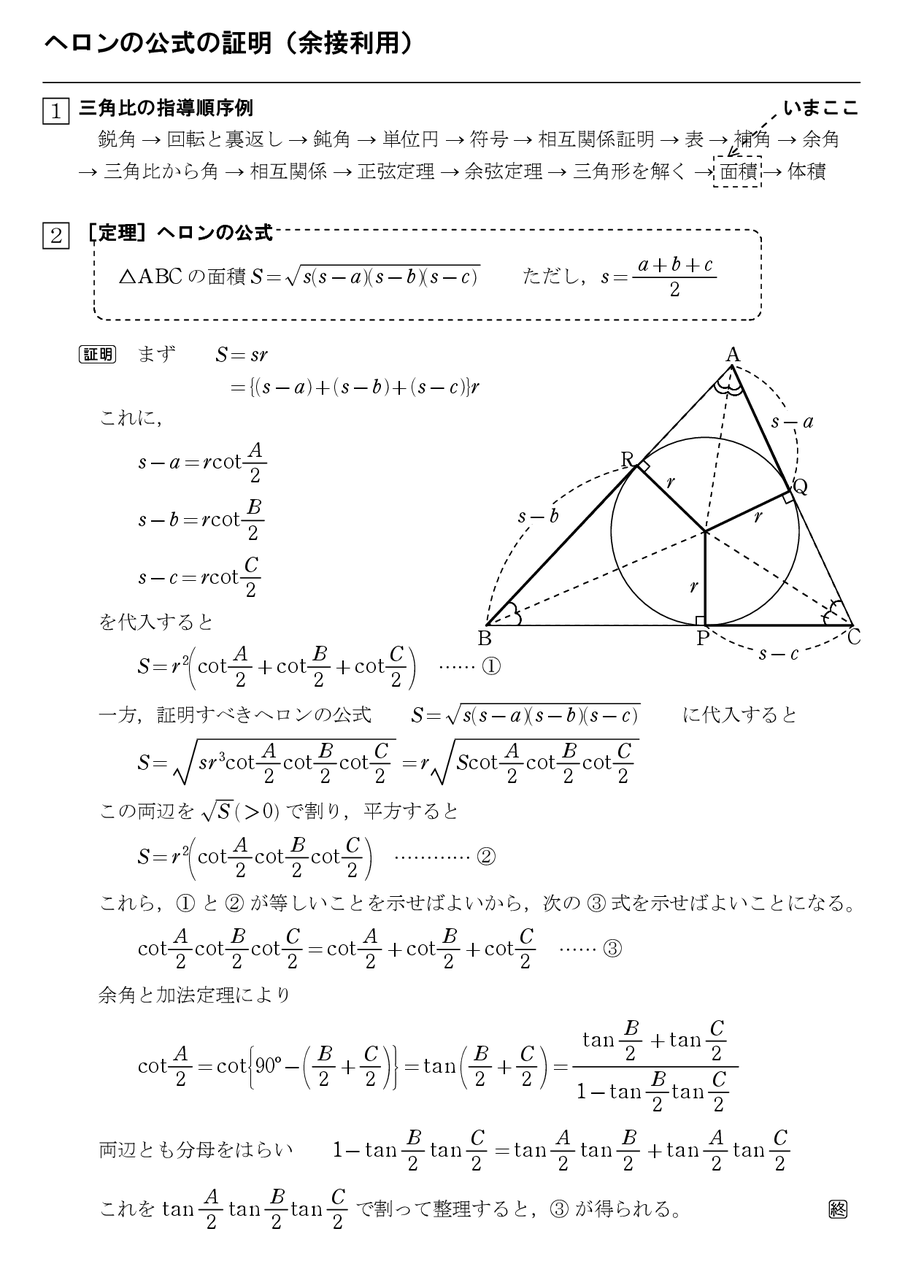



15年08月 怜悧玲瓏 高校数学を天空から俯瞰する




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
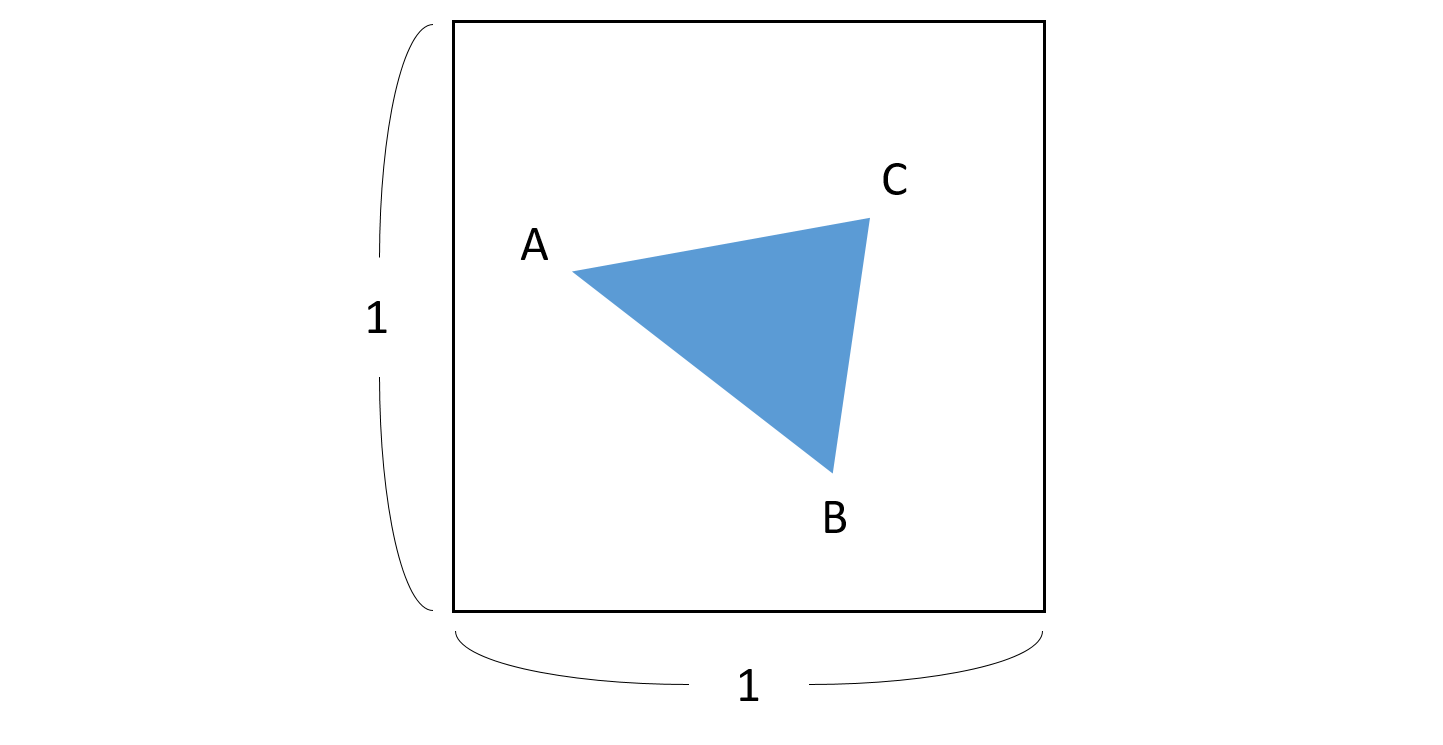



正方形の中にある三角形の面積の平均 Musyokutoumei
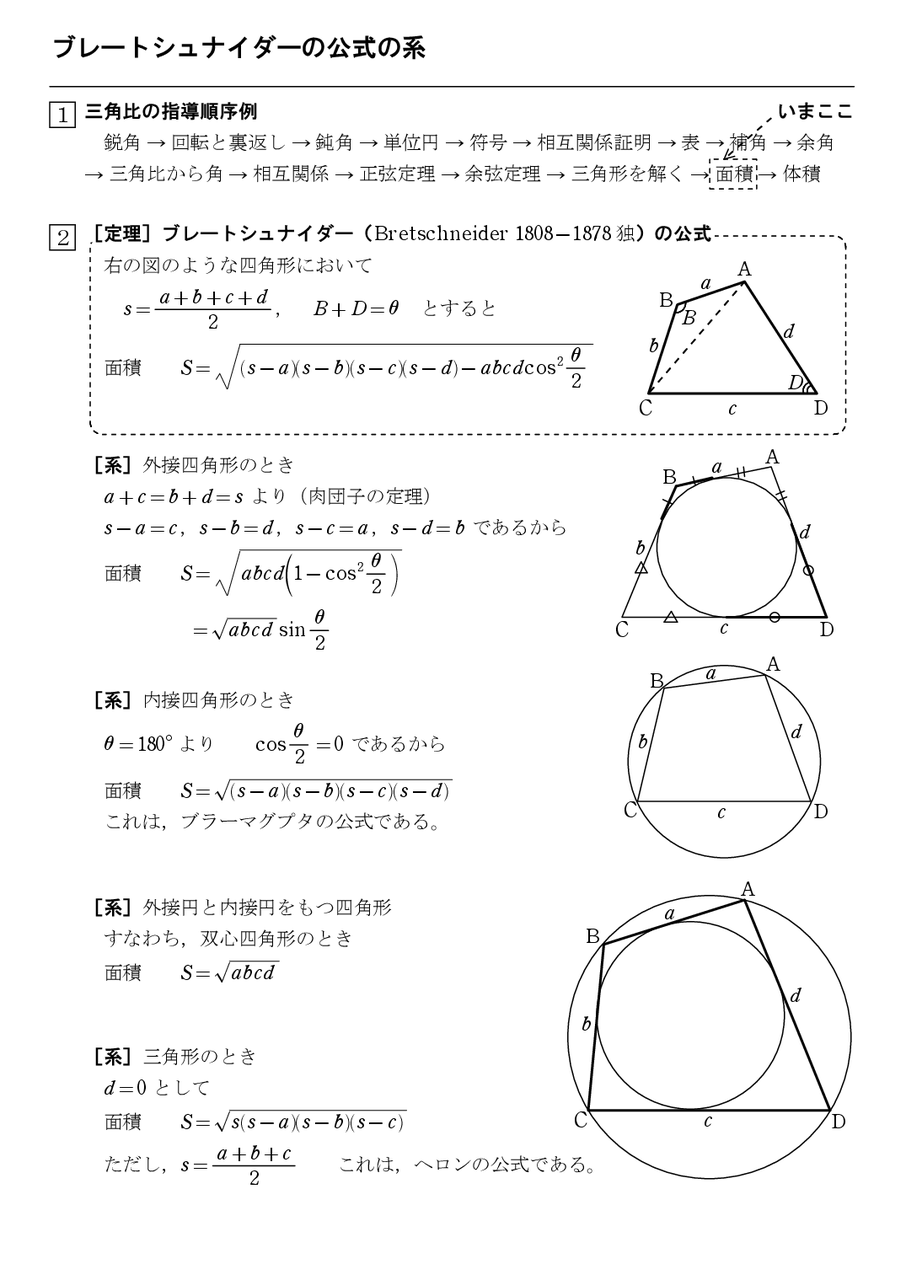



ブレートシュナイダーの公式の系と双心四角形のかき方 怜悧玲瓏 高校数学を天空から俯瞰する




最高 50 正三角形 面積 求め方




三角形の面積 超わかる 高校数学 A 演習 三角比 24 Youtube




ม 4 โน ตของ 数学 円に内接する四角形の面積 北里大学19 Clear



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 円に内接する四角形の対角線の長さと面積 受験の月



Wmhzeavgi2oi8m



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ
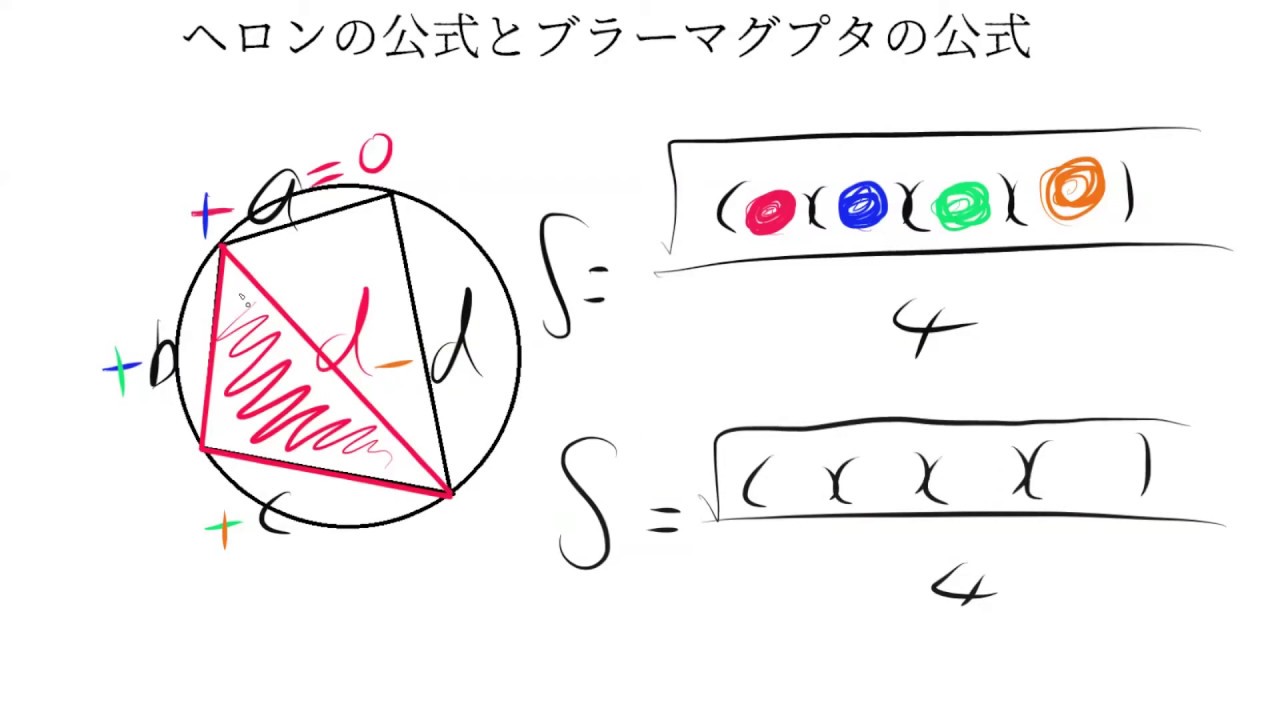



ちょっと中学 高校数学 ヘロンの公式とブラーマグプタの公式 Youtube




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




この答え方を教えてください 答えはgd 4 Pg 6 Clear




三角比 怜悧玲瓏 高校数学を天空から俯瞰する




円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典
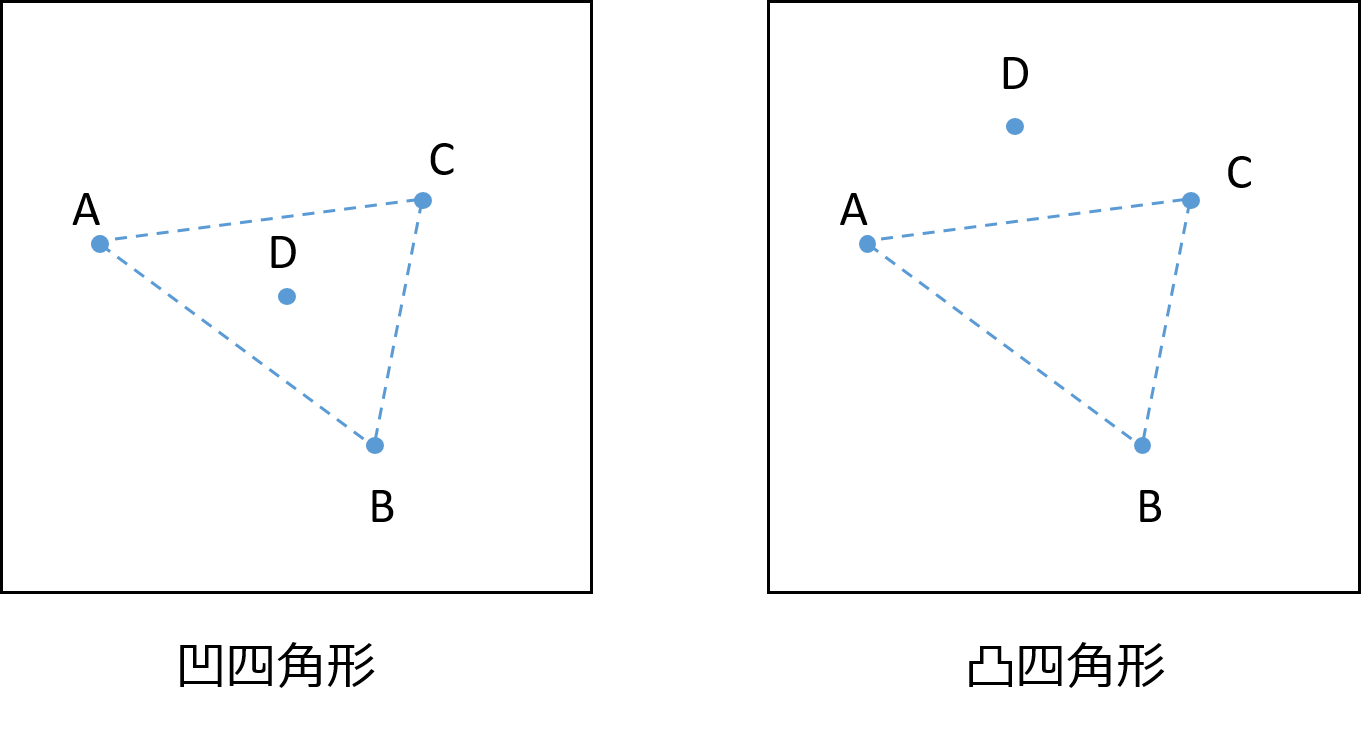



正方形の中にある三角形の面積の平均 Musyokutoumei



最新三角形 の 公式 小学校 最高のぬりえ




ม 4 โน ตของ 数学 円に内接する四角形の面積 北里大学19 Clear




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




史上最強図解 これならわかる 三角関数 ナツメ社
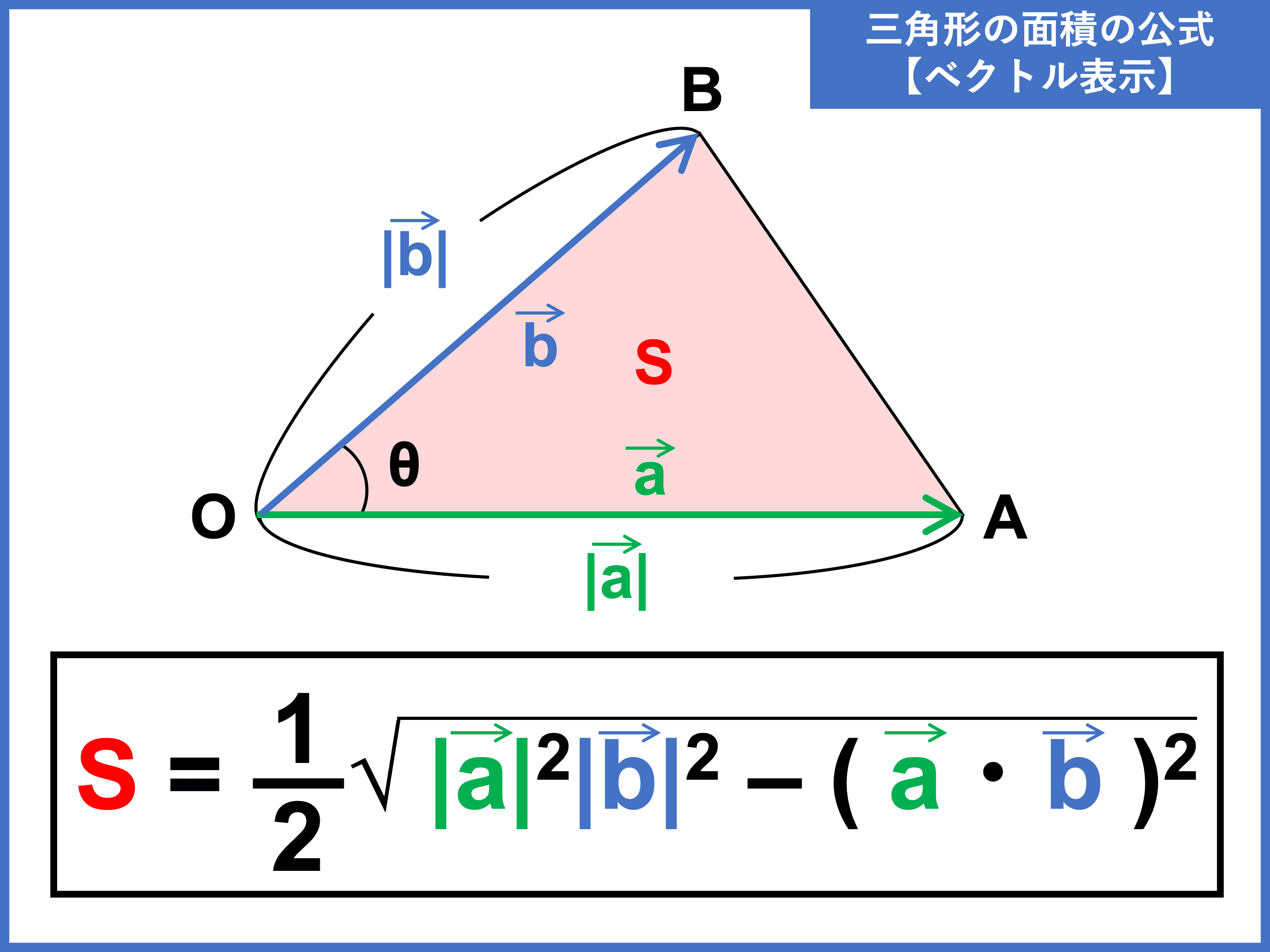



三角関数 面積 公式 証明




三角形の面積と形状 富岡市の総合学習塾 トータルアカデミー




色んな図形の面積の求め方 小学4年の算数の問題です 教科書で確認した Okwave




ヘロンの公式とブラーマグプタの公式をまとめてみました 算数 数学専門塾 算数の極意




79 ヘロンの公式 三角形と内接四角形 両方解説 ブラーマグプタの公式 Youtube




円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません




ブラーマグプタの公式 東大合格コム



ヘロンの公式 まなびの学園




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月




新鮮な四角形 対角線 長さ 求め方 最高のぬりえ




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート




高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月
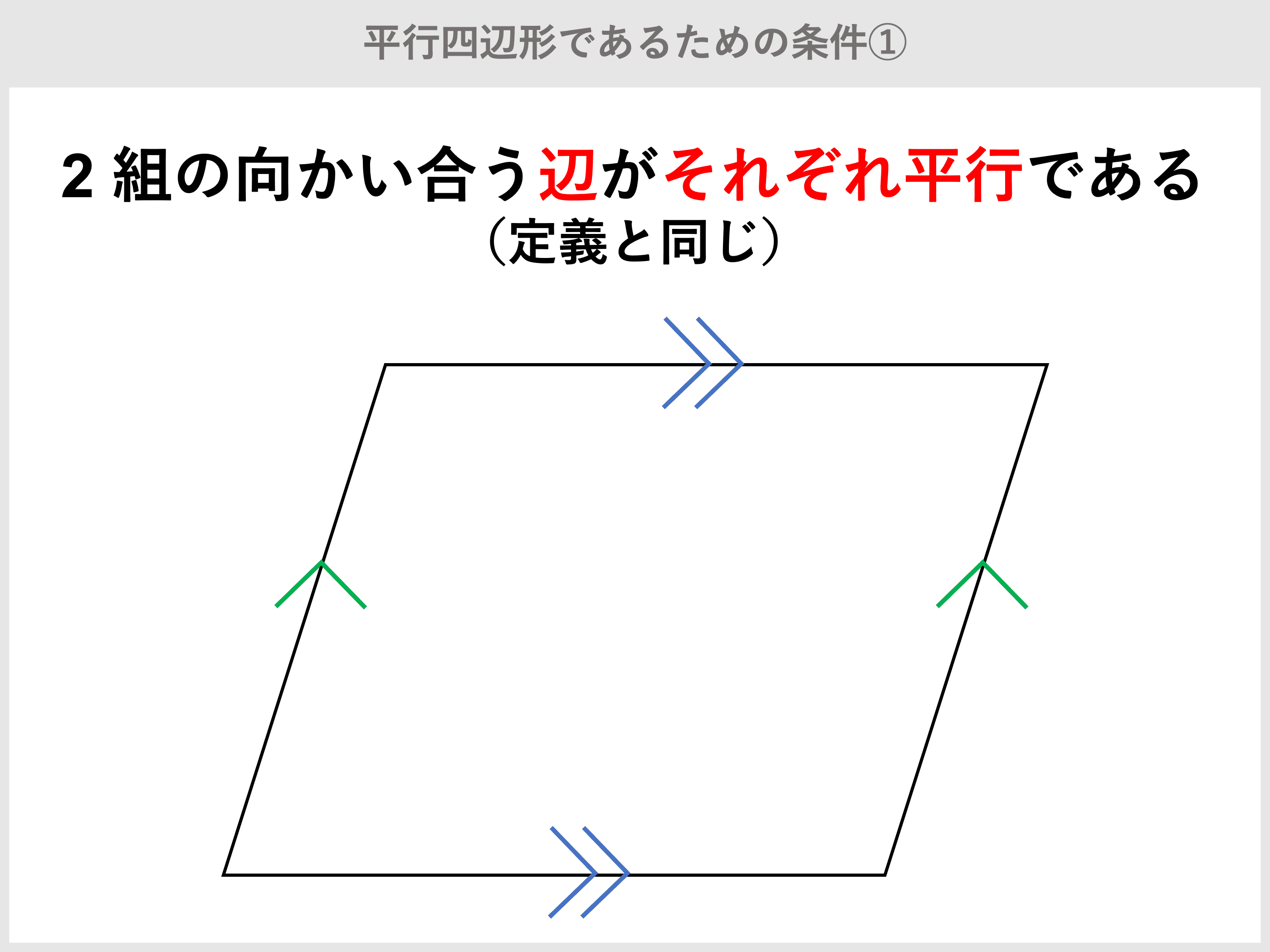



トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート



Yukijinet ヘロンの公式を利用した4辺から面積を割り出す計算機



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




三角比の添削 追記9月14日 Matsu Math Note




内接四角形の面積とヘロンの公式 小ネタ集 テストにでるすぐに使える数学のウラ技 Youtube
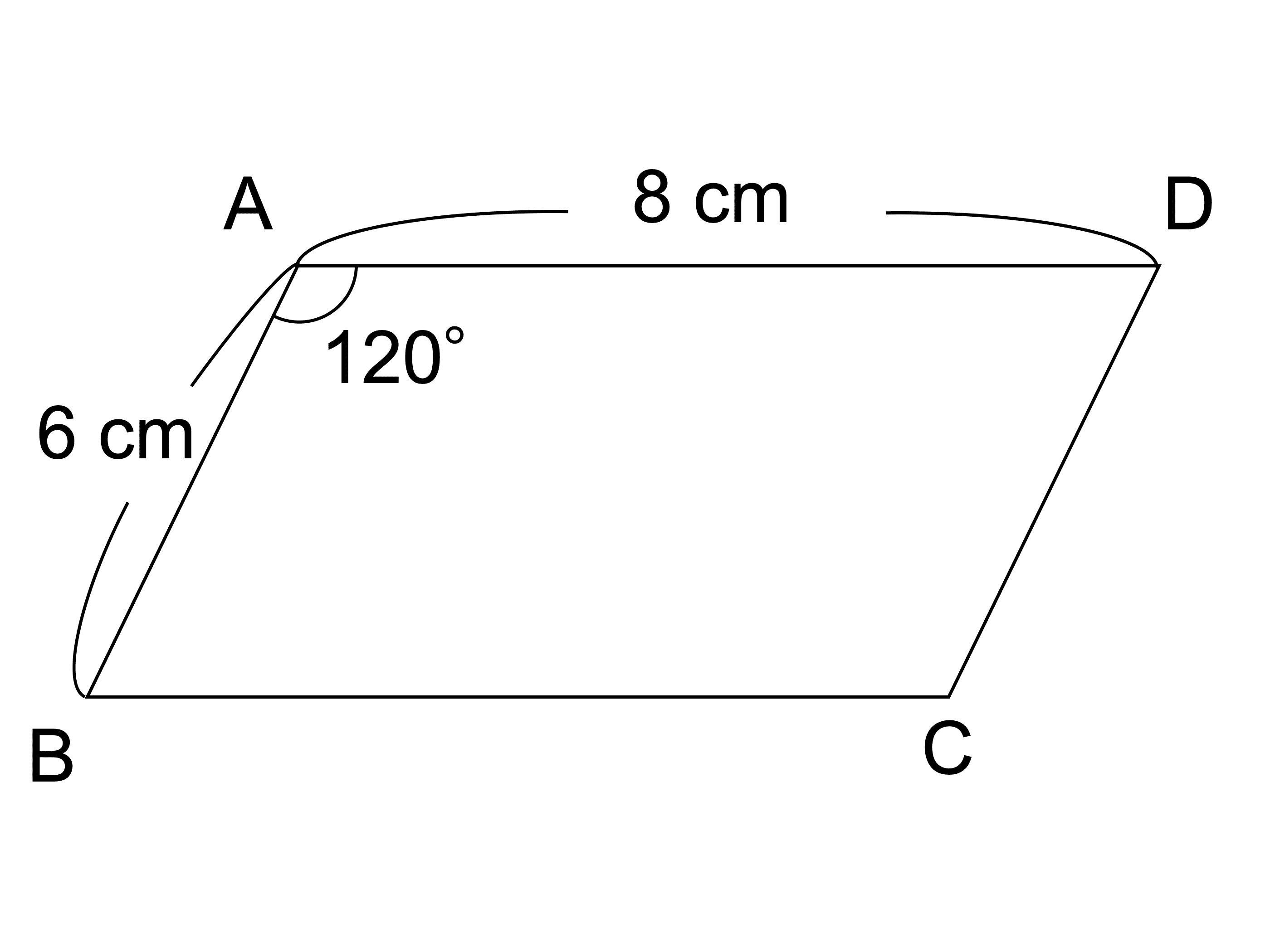



トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ




数学検定1級合格者が解説 ブラーマグプタの面積の公式の覚え方 一瞬で覚える語呂合わせ 公式を覚えよう 数検 Youtube
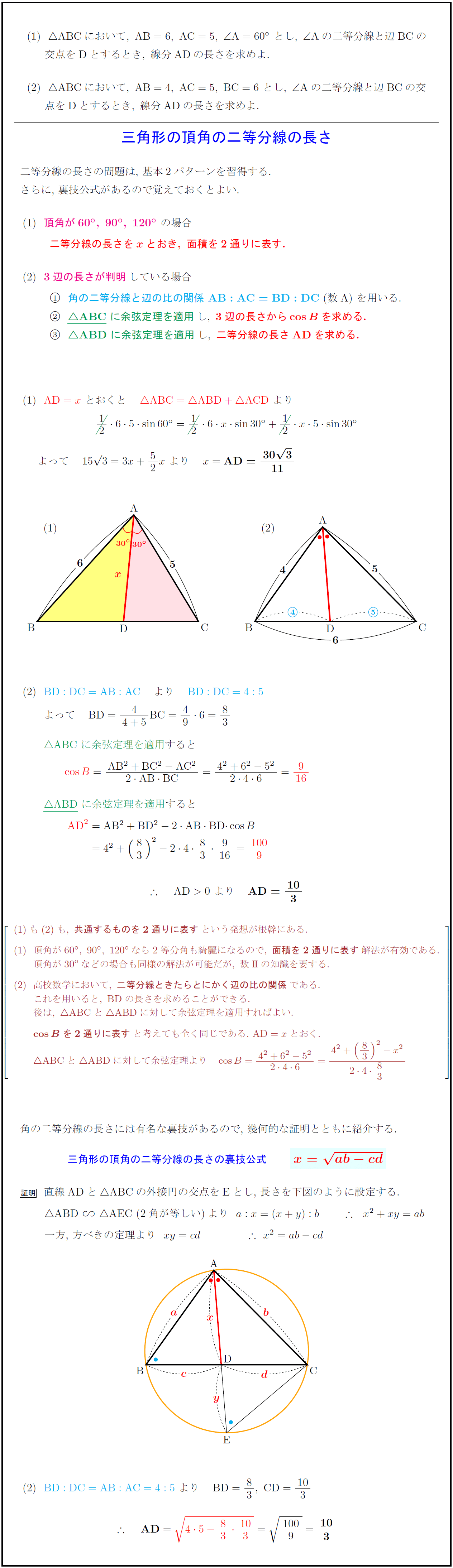



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
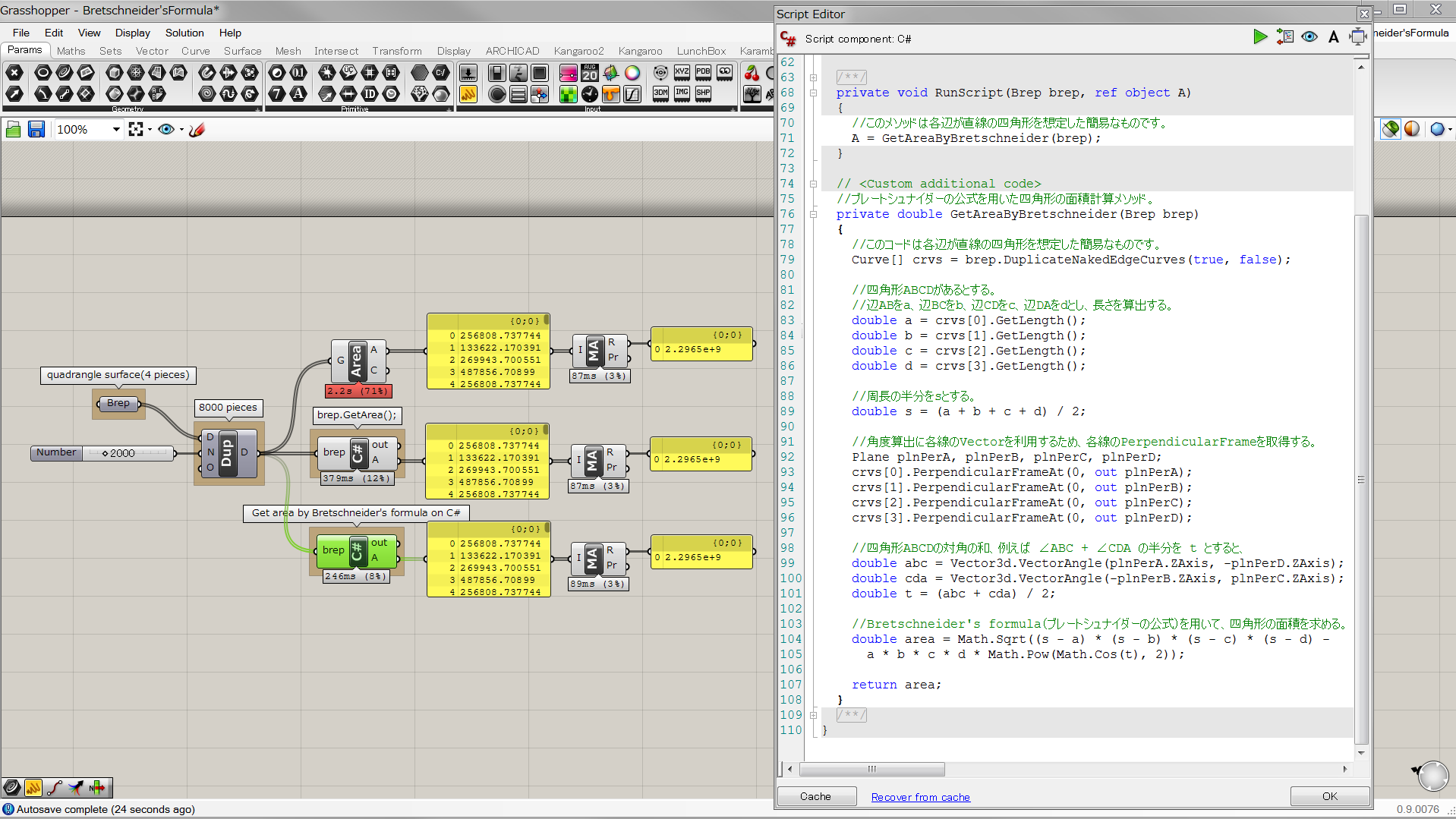



Openddl Digital Designに関する共有サイト




の問題の 青でマークした部分以降についてです Clear




ブラーマグプタの公式




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月




三角形 Wikipedia




ブレートシュナイダーの公式 Wikipedia
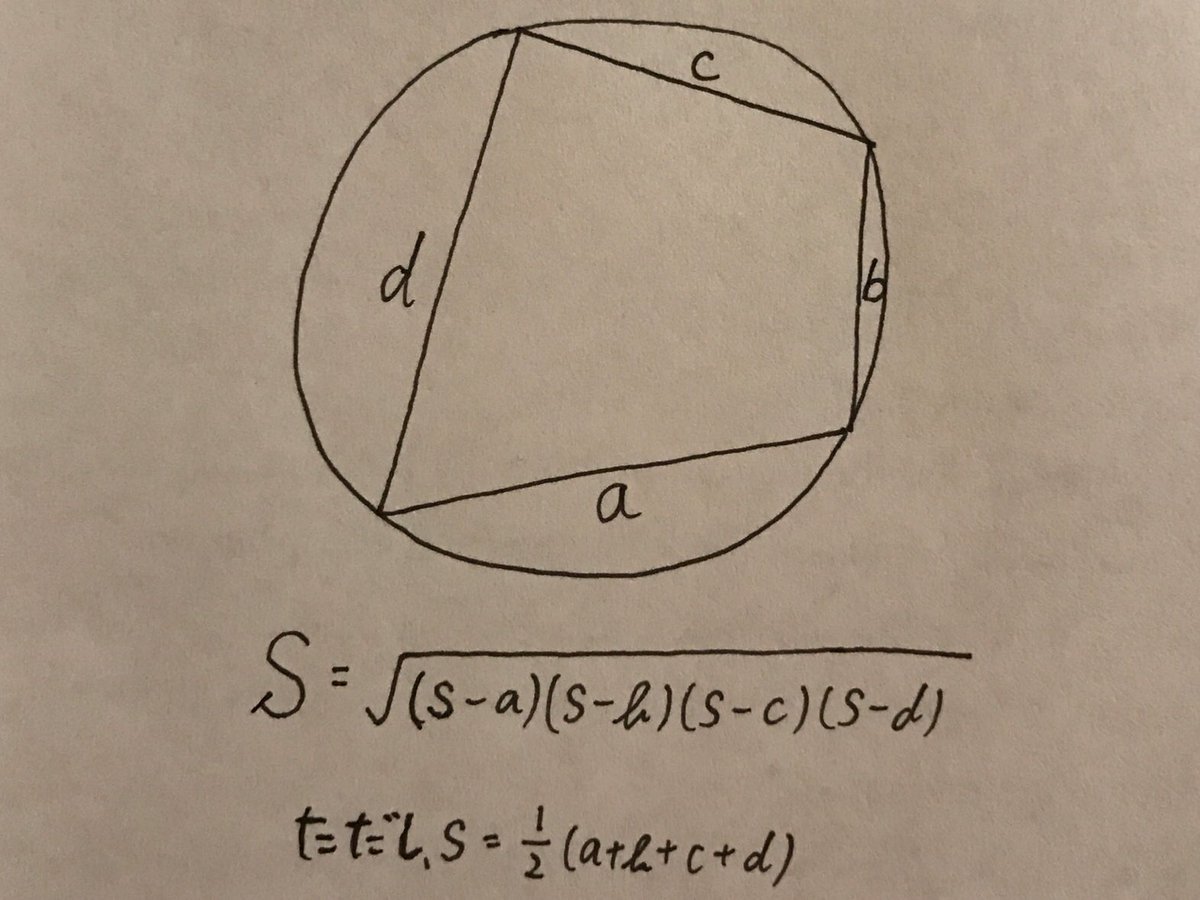



Cancelo 円に内接する四角形の面積sを求めてるなうに使っていいよ No Twitter




改訂版 教科書傍用 3trial 数学a チャート式の数研出版



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース




三角比の面積 公式と計算方法は いろんな場面での使い方を解説 数スタ




高校数学 三角比 円に内接する四角形の面積求め方まとめと問題



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




三角比の添削 追記9月14日 Matsu Math Note



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




最新三角形 の 公式 小学校 最高のぬりえ




高校数学 数 94 三角形の面積 ヘロンの公式編 Youtube
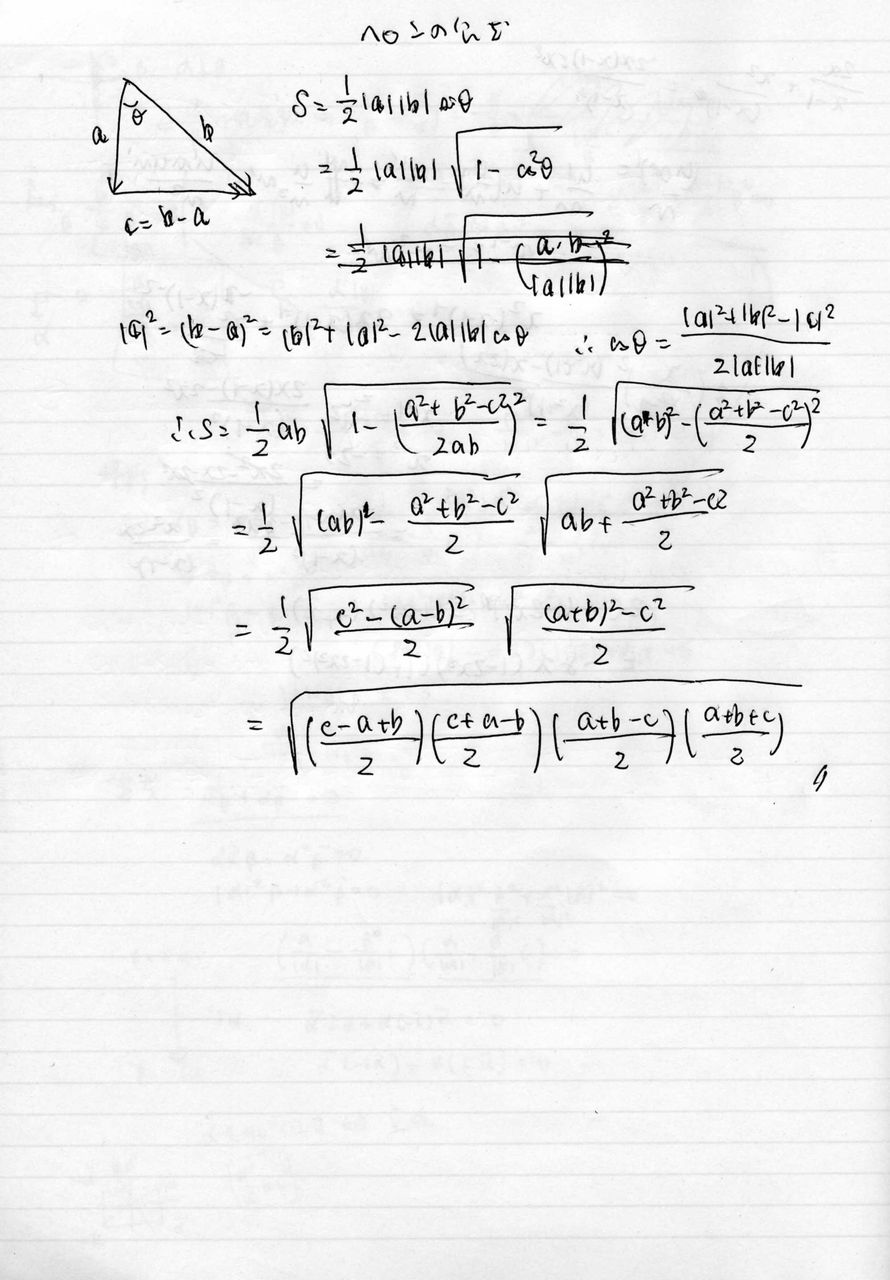



17年08月24日 東大合格コム



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




速報 19年 立命館大学 薬学方式 数学 第1問 ますいしいのブログ
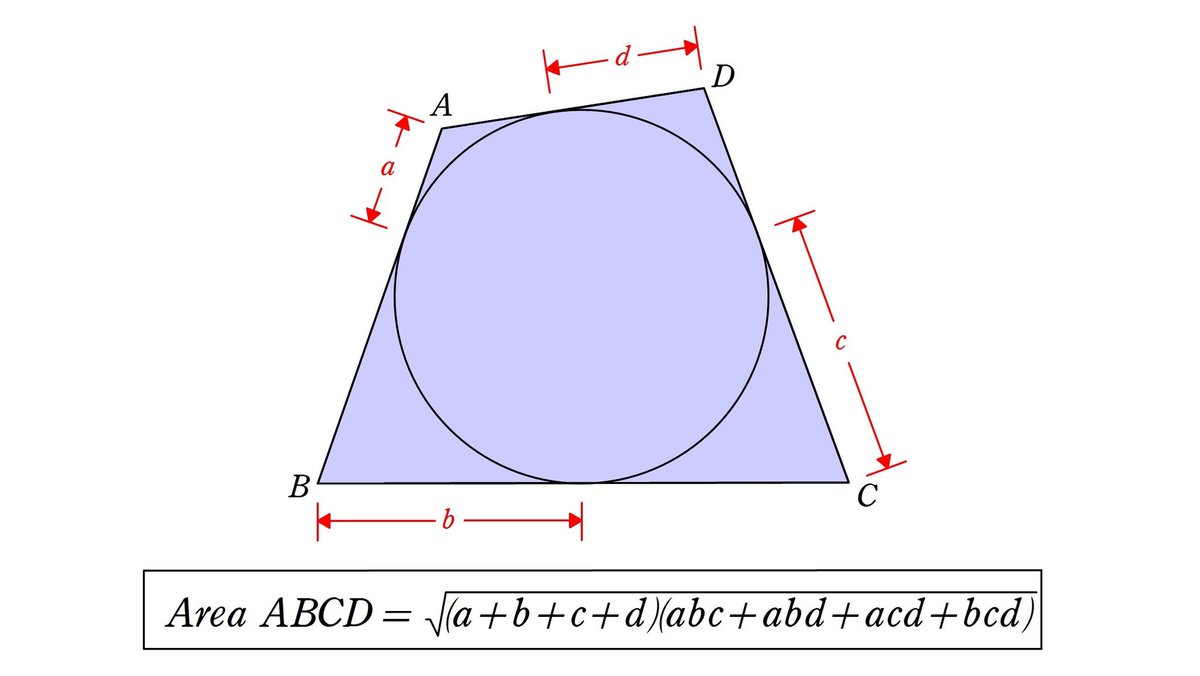



ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません




三角比 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




ブラーマグプタ Brahmagupta 598年 668年 Institute Of Reproducing Kernels




円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




28hmdbcvx1zgvm




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート



0 件のコメント:
コメントを投稿