Conic Sections (see also Conic Sections) Point x ^2 y ^2 = 0 Circle x ^2 y ^2 = r ^2 Ellipse x ^2 / a ^2 y ^2 / b ^2 = 1 Ellipse x ^2 / b ^2 y ^2 / a ^2 = 1 Hyperbola x ^2 / a ^2 y ^2 / b ^2 = 1 Parabola 4px = y ^2 Parabola 4py = x ^2 Hyperbola y ^2 / a ^2 x ^2 / b ^2 = 1 For any of the above with a center at (j, k) instead of (0,0), replace each x term with (xj) and(x2 −3x)dx = x3 3 − 3x2 2 5 3 = 125 3 − 3×25 2− 27 3 − 3×9 2 = 412 3 − 37 1 2 − 913 2 = 3 So the total actual area is 41 2 3 = 131 6 units of area Example Find the area bounded by the curve y = x2x4, the xaxis and the ordinates x = 1 and x = 3 Solution If we set y = 0 we obtain the quadratic equation x2 x 4Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
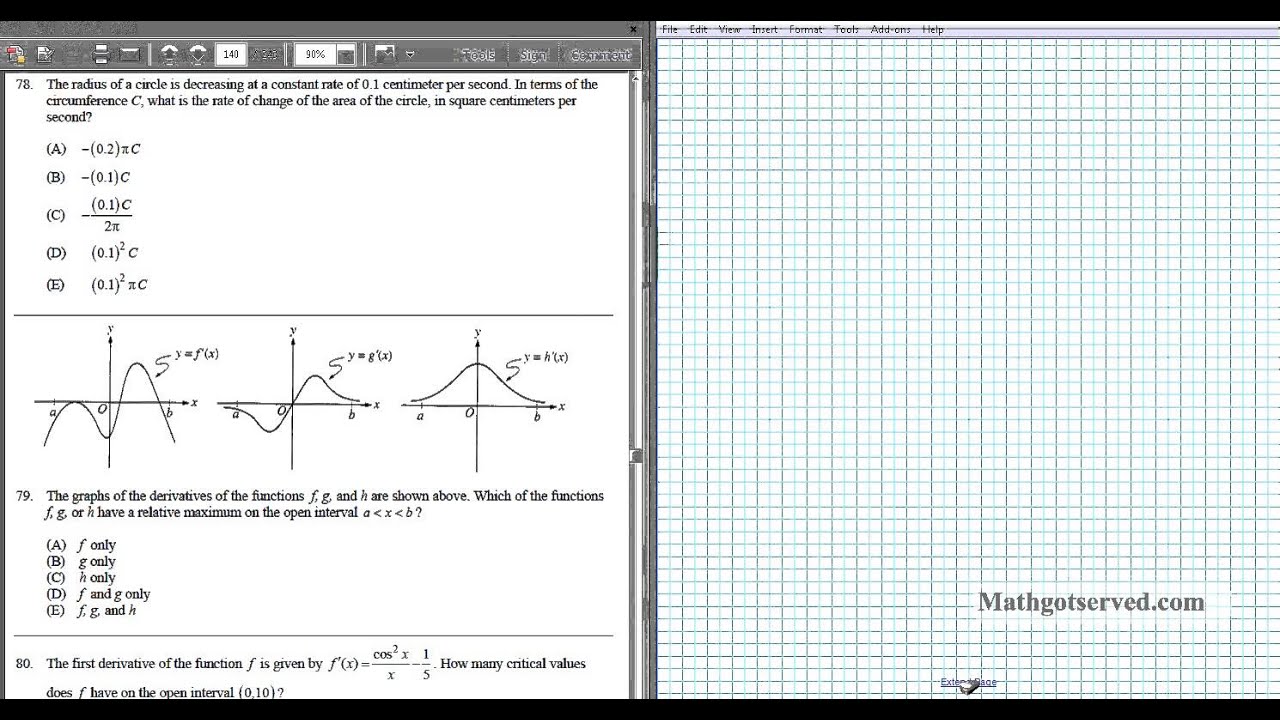
Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
Y=(x^2-5)(x-1)^2(x-2)^3 graph
Y=(x^2-5)(x-1)^2(x-2)^3 graph-Divide 2, the coefficient of the x term, by 2 to get 1 Then add the square of 1 to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}2x1=y41 Square 1 x^ {2}2x1=y3 Add y4 to 1 \left (x1\right)^ {2}=y3 Factor x^ {2}2x1Explanation Question y = x 2 5x 6 Work The factors of 6 are 1 and 6 2 and 3 3 and 2 6 and 1 1 and 6 2 and 3 and so on Now, which one adds
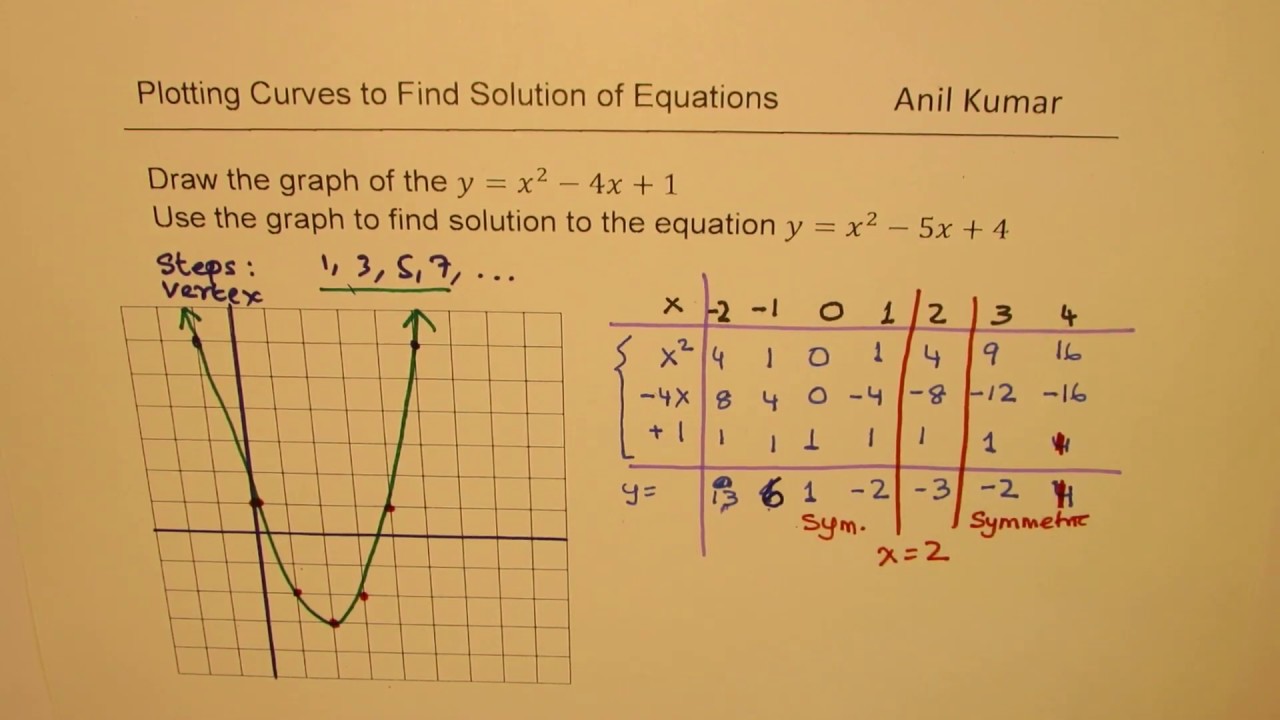


Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube
· The distance squared from there to (3,0) is (x 3)^2 (x^1/2 0)^2 = (x 3)(x3) (x^1/2)^2 = x^2 6x 9 x = x^2 5x 10 If y = ax^2 bx c, and a > 0, the minimum happens when x = b / (2a) so x = (5) / (2•1) = 5/2 = 25 so the point is (25, √25) (or, if you are in calculus, just do the derivative and set it = 0 2x 5Example (x−1)/(x 2 −9) On the page Rational Expressions we do some work to discover that the function crosses the xaxis at 1, crosses the yaxis at 1/9, has vertical asymptotes (where it heads towards minus/plus infinity) at −3 and 3; · It is a U shaped a parabola as a > 0 x vertex = − b 2a = −0 2 = 0 y = 0 5 = 5 Vertex(0,5) Two points x = 1 y = 12 5 = 6 ⇒ (1,6) x = − 1 y = ( − 1)2 5 = 6 ⇒ ( − 1,6) Find the three points and the graph looks like this https//wwwdesmoscom/calculator/qwjal4zmxo Answer link
The graph of f x =1 2 (1 4) x2 4 f x =1 2 (1 4) x2 4 is shifted downward 4 4 units, and then shifted left 2 2 units, stretched vertically by a factor of 4, 4, and reflected about the xaxis What is the equation of the new function, g (x)?Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be moved down by 2 units So we just take our first curve and move it down 2 units Our new curve's vertex is at −2 on the yaxisGiven , mathy = (x2)(x3)(x1) = x^{3} 4x^{2} x 6/math Now , At mathx = 0 , y = 6/math At mathy = 0 , x = 1 , 2 , 3/math So the graph of the given
, yintercept is found by putting x = 0 in the equation y = 2x2 _ x − 3 or y = −3 y intercept is at (0, − 3) · So, the slope of the tangent line there will be 1 Now, we use the pointslope formula to figure out the equation of the line, that is y − y0 = m(x − x0) where m is the slope of the line, (x0,y0) are the original coordinates And so, y − ( − 4) = 1(x − 3) y 4 = x −3 y = x −3 −4 y = x −7Play this game to review Algebra I A golfer hit a golf ball from a tee box that is 6 yards above the ground The graph shows the height (in yards) of the golf ball above the ground as a quadratic function of x Where x is the horizontal distance (in yards) of the golf ball from the tee box What is the domain of the function for this situation?



Draw The Graph Of The Equation X Y 3 And Y X 1 What Do You



Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
· y = a(x − h)2 k;(h,k) being vertex , here h = − 025,k = −3125,a = 2 , therefore vertex is at ( − 025, − 3125), since a is positive, parabola opens upward Axis of symmetry is x = h or x = − 025; · precalculas write a function whose graph is the graph of y=x^2, but is shifted to the left 6 units Algebra please check my answers 2 how is the graph of y=6x^24 different from the graph of y=6x^2 A it is shifted 4 units to the left B it is shifted 4 units to the right C it is shifted 4 units up**** Dit is shifted 4 units downThe graph of y=2/3x represents a graph of a linear function On the given graph you can find all of the important points for function y=2/3x (if they exist)


Graph Y X 2 3 Youtube


Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find T
1plot x^2 2invert it about x axis 3raise it upwards by 1 unit 4This is y=1x^2 5for mod(y), along with this, take mirror image about x axis 6Combined graph is the solutionState its yintercept, domain, and rangeI want to graph the curve of y=(4x^2)^5 without using a graphing calculator To do this, I'm suppose to find domain, y and x intercepts, asymptotes, intervals of increase/decrease, local max/min, concavity and points of inflection I got all the way to the step where I'm solving the concavity and I'm stuck



Differentiation Questions And Answer Derivative Tangent



Identify The Graph Of The Equation X 2 2 Y 5 2 4 Brainly Com
Trigonometry Graph y=2 (x1)^25 y = −2(x − 1)2 5 y = 2 ( x 1) 2 5 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 2 a = 2 h = 1 h = 1 k = 5 k = 5Plotting graphics3d Share Improve this question Follow asked Nov 29 '15 at 533 user userDivide \frac{3}{y1}, the coefficient of the x term, by 2 to get \frac{3}{2\left(y1\right)} Then add the square of \frac{3}{2\left(y1\right)} to both sides of the equation



Which Of The Following Graphs Represents The Equation Y 2 3 X 1 Brainly Com
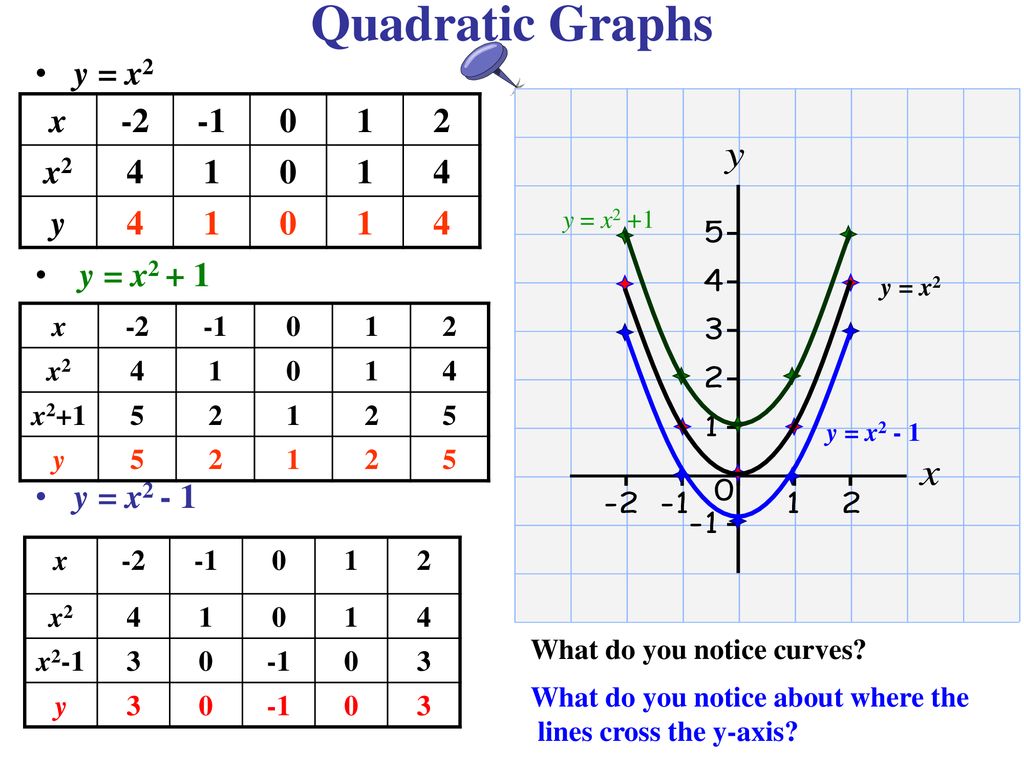


Quadratic Graphs Parabolas Ppt Download
Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;Cos(x^2) (x−3)(x3) Zooming and Recentering You can clickanddrag to move the graph around If you just clickandrelease (without moving), then the spot you clicked on will be the new center To reset the zoom to the original click on the Reset button Using "a" ValuesSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Reflecting Functions Examples Video Khan Academy



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube
Observe that when the function is positive, it is symmetric with respect to the equation $\mathbf{y = x}$Meanwhile, when the function is negative (ie, has a negative constant), it is symmetric with respect to the equation $\mathbf{y = x}$ Summary of reciprocal function definition and properties Before we try out some more problems that involve reciprocal functions, let's · Depends what you want to know if y = x^2 5 You could make a table of coordinates for x and y and draw a graph Intercepts on x and y axis are when y = 0 and x = 0 respectivelyHow to plot 3 dimensional graph for x^2 y^2 = 1?



Use A Single Graph And Draw The Graph Of The Following Equations 2y X 8 5y X 14 Y 2x 1 Obtain The Brainly In



Finding Inverse Functions Quadratic Example 2 Video Khan Academy
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyI am already using it and I only can plot in 2 dimensional graph Can someone help me with this problem?Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
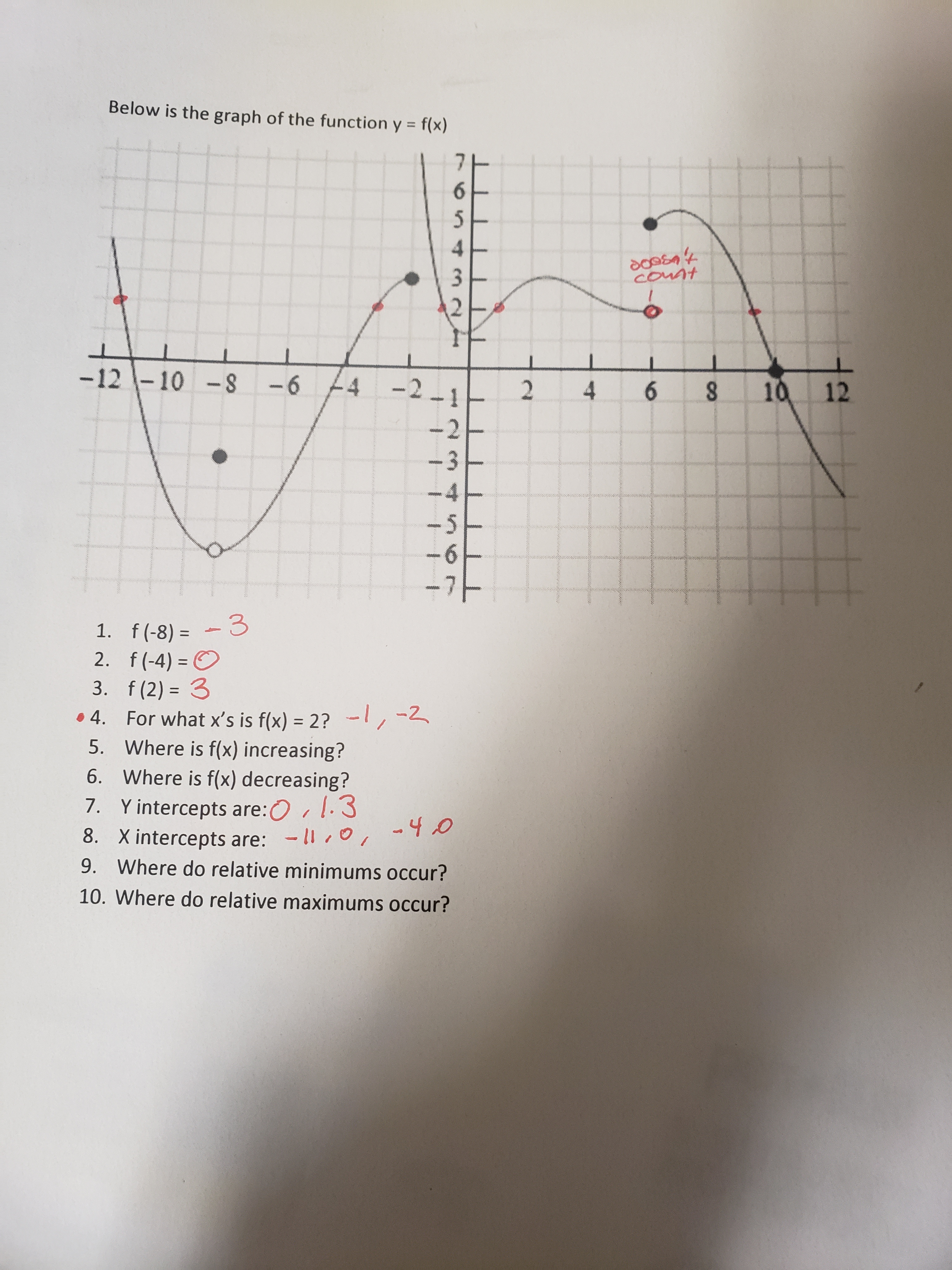


Answered Below Is The Graph Of The Function Y Bartleby



Graph By Plotting Points
Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with 1 1 in the expression f ( 1) = − ( 1) 2 5 ( 1) − 3 f ( 1) = ( 1) 2 5 ( 1) 3 Simplify the result · You can use any value for X & Y that satisfies the equation but make sure that the value you take is simple & sober so that it does not cross the limit of coordinate axes I hope that you know that you have to atleast take two points to make a line Example y=x^25 x^2y = 5 x = 0 , y = 5 & x = 1 , y = 6Graph y=x^25 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola
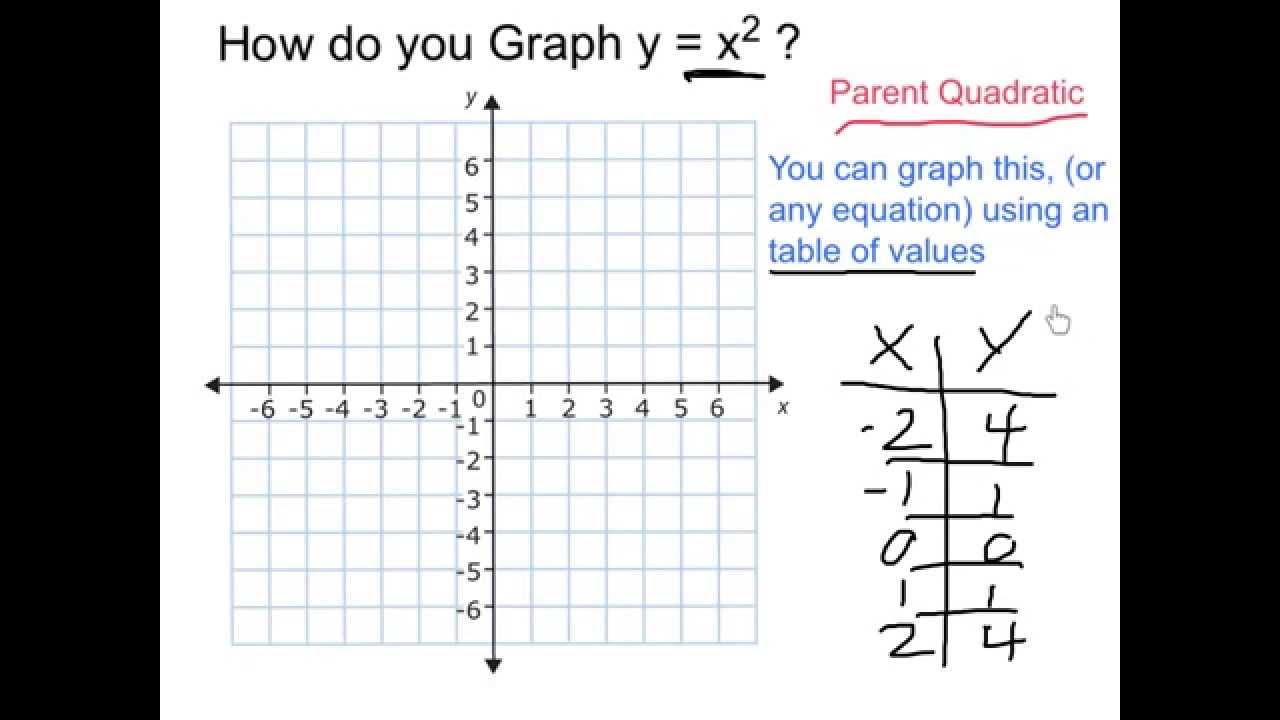


Graph Y X 2 Youtube
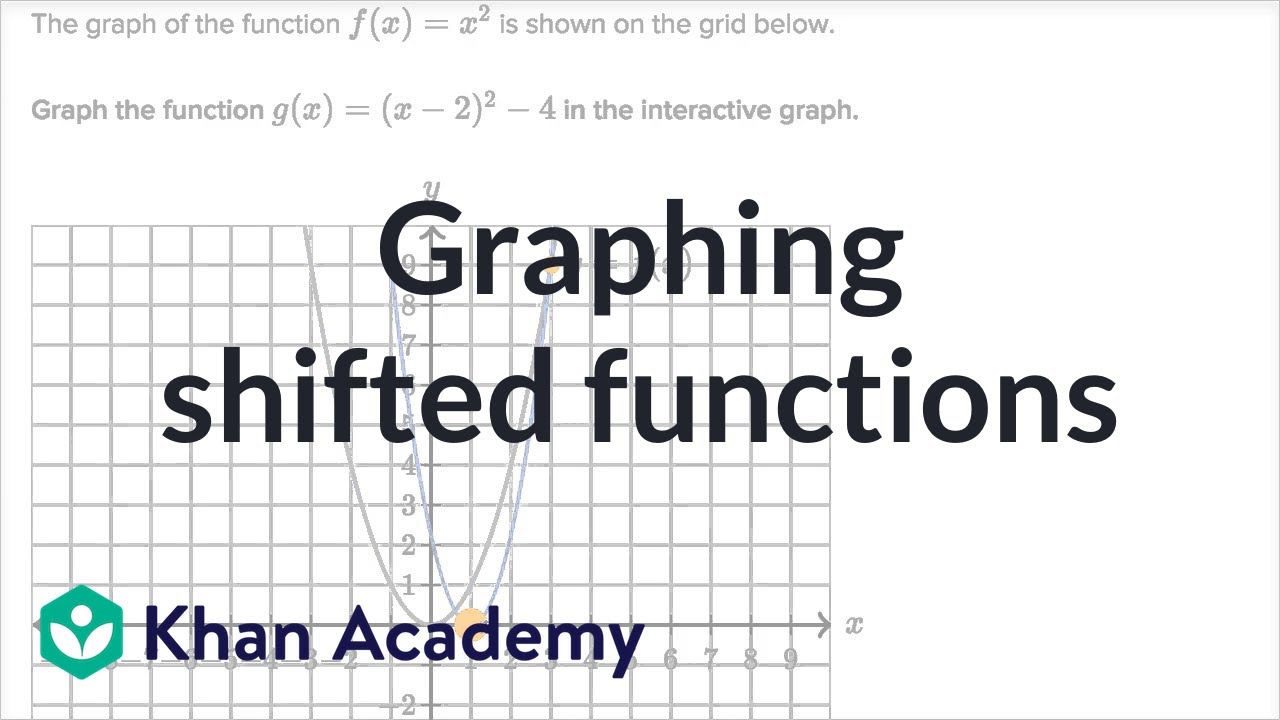


Graphing Shifted Functions Video Khan Academy
Solve for y y=x^ {5}x^ {3}x^ {2}1 y = x5 x3 − x2 − 1 View solution steps Solution Steps y = ( x ^ { 2 } 1 ) ( x ^ { 3 } 1 ) y = ( x 2 1) ( x 3 − 1) Use the distributive property to multiply x^ {2}1 by x^ {3}1 Use the distributive property to multiply x 2 1 by x 3 − 1 · 0 = x² x 2 x² x 2 = 0 (x 2)(x 1) = 0 x = 2, x = 1 Thus, the xintercepts are 2 and 1 (iii) This function is a parabola, and it has its equation in the form y = (x h)² k The vertex, in this form, is (h,k) Try converting your function to this form(use completing the square) y = x² x 2 y = x² x 1/4 2 1/4 · Given #y = x^3 x^2 5x# You can use the first derivative test or the second derivative test The second derivative test is straight forward if the second derivative is easy to find It does not require setting up intervals and testing a value in each interval Using the Second Derivative Test #f(x) = x^3 x^2 5x# #f'(x) = 3x^2 2x 5#



Transforming Exponential Graphs Example 2 Video Khan Academy
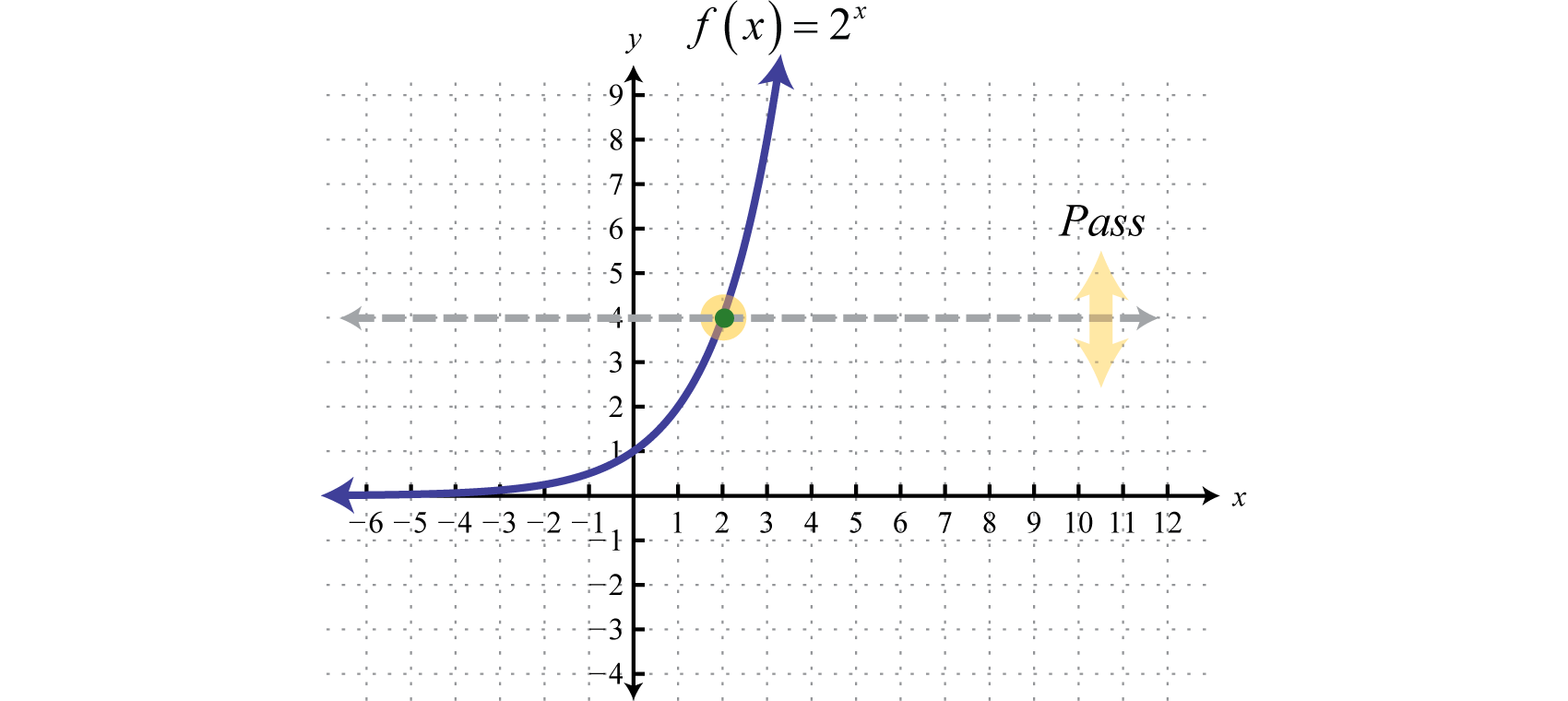


Logarithmic Functions And Their Graphs
C < 0 moves it downGraph $$4 xy=6$$ AG Ankit G Numerade Educator Like Report Jump To Question Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6 Problem 7 Problem 8 Problem 9 Problem 10 Problem 11 Problem 12 Problem 13 Problem 14 Problem 15 Problem 16 Problem 17 Problem 18 Problem 19 Problem Problem 21 Problem 22 Problem 23 Problem 24 ProblemThe result is that we can make this sketch Sketch of (x−1)/(x 2 −9) from Rational Expressions
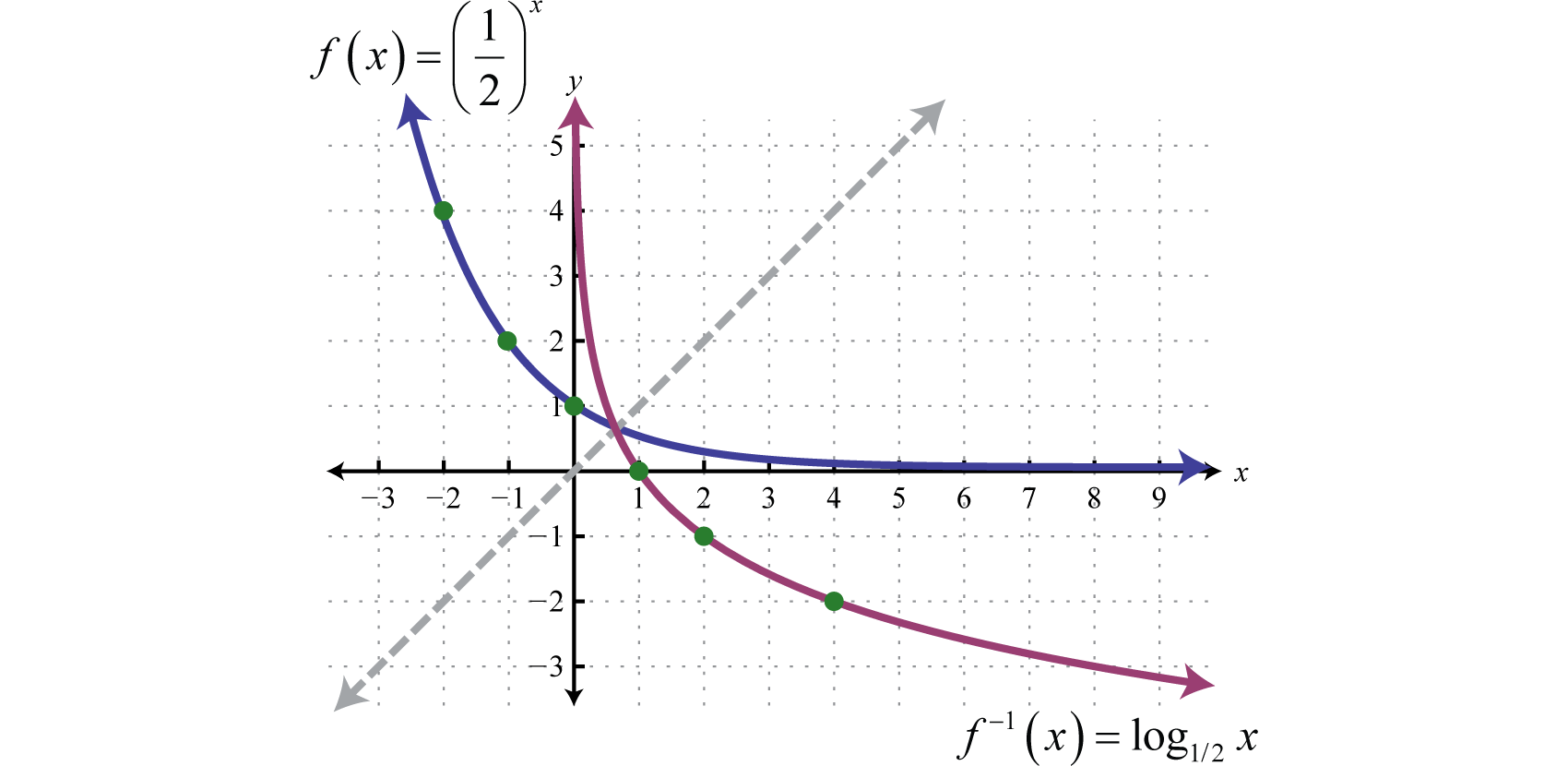


Logarithmic Functions And Their Graphs
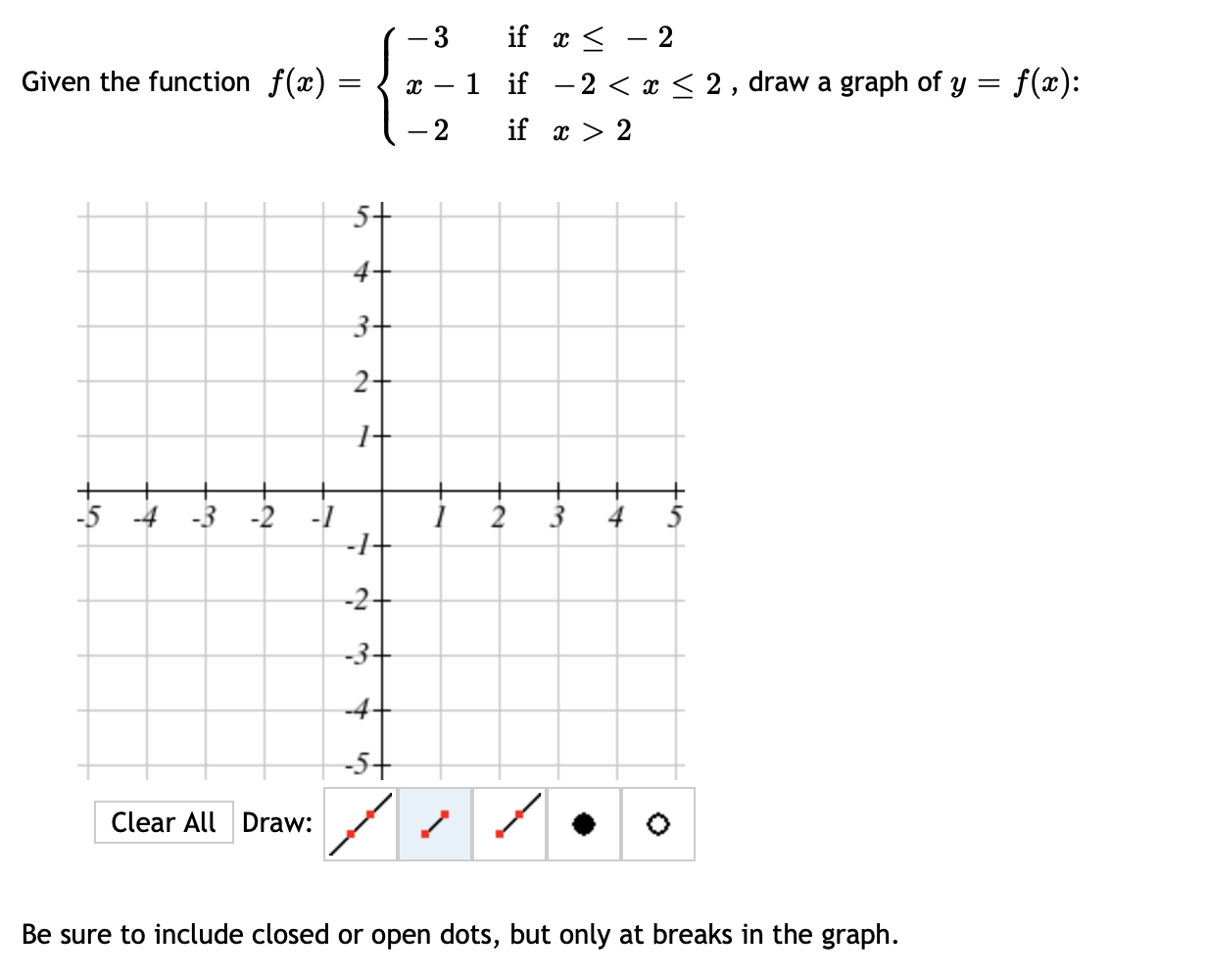


Solved 1 3 If X 2 Given The Function F X X 1 I Chegg Com
1 (a) Simplify 1 3 2 2 2 − − − x x x (3) (b) Hence, or otherwise, express 1 3 2 2 2 − − − x x x – ( 1) 1 x x as a single fraction in its simplest form (3) 2 Figure 1 Figure 1 shows the graph of y = f (x), 1 < x < 9 The points T(3, 5) and S(7, 2) are turning points on the graph · I know this because the graph of x^2 is a parabola The minus 5 part means a vertical shift If you meant x = y^2 5, then first solve for y Add 5 to both sides > x 5 = y^2 Now square root both sides > sqrt (x 5) = y The graph of y = sqrt (x 5) is a sideways parabola opening to the right with the vertex shifted 5 units to the leftAlgebra Graph x^2y^2=5 x2 y2 = 5 x 2 y 2 = 5 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yoffset from origin


How Do You Find An Equation Of The Tangent Line To The Graph F X X 2 2x X 1 At 1 6 Socratic



Teaching X And Y Axis Graphing On Coordinate Grids Houghton Mifflin Harcourt
Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yGraph x/2 3Graph halfx 3(x1)/3x2=(x2)/2x3 Two solutions were found x =(8√184)/2=4√ 46 = 107 x =(8√184)/2=4√ 46 = 27 Rearrange Rearrange the equation by


Draw The Graph Of The Equation X 2y 4 Use Graph To Find Br



How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorSOLUTION 4 Begin with y = x 2 y 3 x 3 y 2 Differentiate both sides of the equation, getting D(y) = D ( x 2 y 3 x 3 y 2) , D(y) = D ( x 2 y 3) D ( x 3 y 2) , (Use the product rule twice) , (Remember to use the chain rule on D ( y 3) and D ( y 2) ) , y' = 3x 2 y 2 y' 2x y 3 2x 3 y y' 3x 2 y 2, so that (Now solve for y' ) y' 3xWhen x = 0, y = 5 when y = 0, x^2 = 5, so x = set up some points from x = 5 to x = 5 x,y5,4,113,42,11,4 0,5 1,4 2,1 3,4 4,11 5, looks like the graph bottoms out at 5 and goes up symmetrically for every value of /1 x graph would look like this



Example 7 Let A 1 2 3 4 5 6 R X Y Y X 1
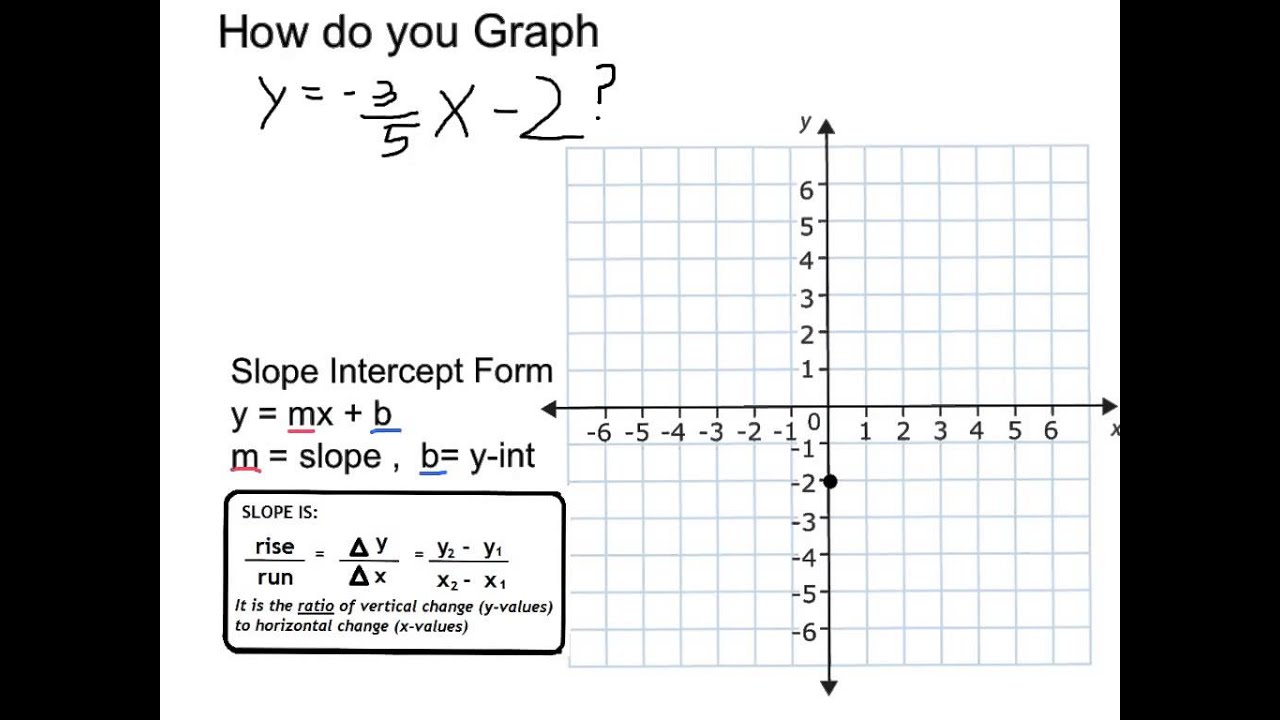


Graph Y 3 5 X 2 Youtube
Graph x^2y^2=1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive Simplify each term in the equation in order to set the right side equal to The standard form of an ellipse or hyperbola requires the right side of the equation beThe graph of f(x)=1/x3 is a visual presentation of the function in the plane On the given graph you can find all of the important points for function f(x)=1/x3
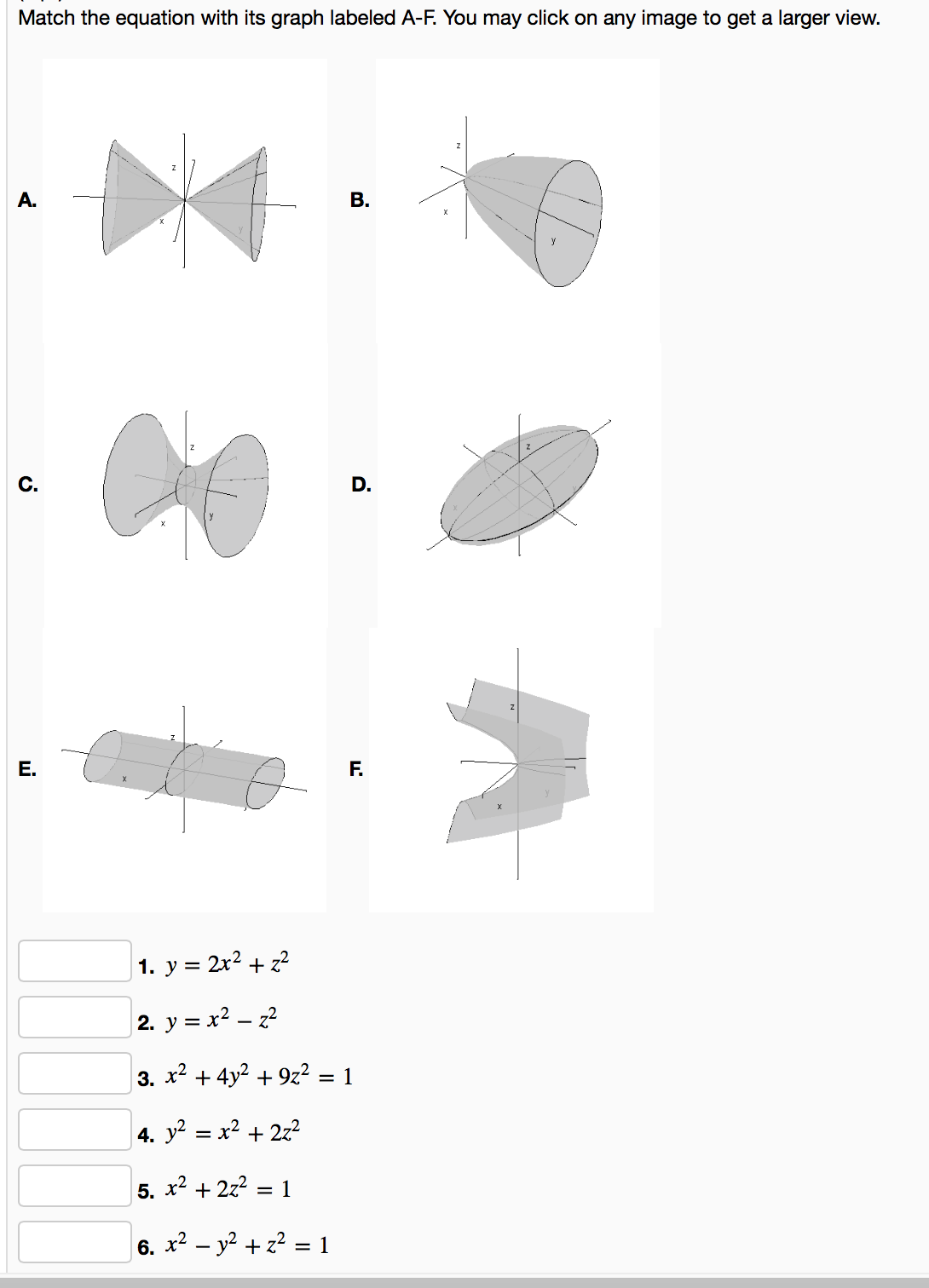


Solved Match The Equation With Its Graph Labeled A F You Chegg Com



Ex 6 3 11 Solve 2x Y 4 X Y 3 2x 3y 6



Bellwork Graph Each Line 1 3x Y 6 2 Y 1 2 X 3 Y Ppt Video Online Download



Chapter 1 Practice Exercises
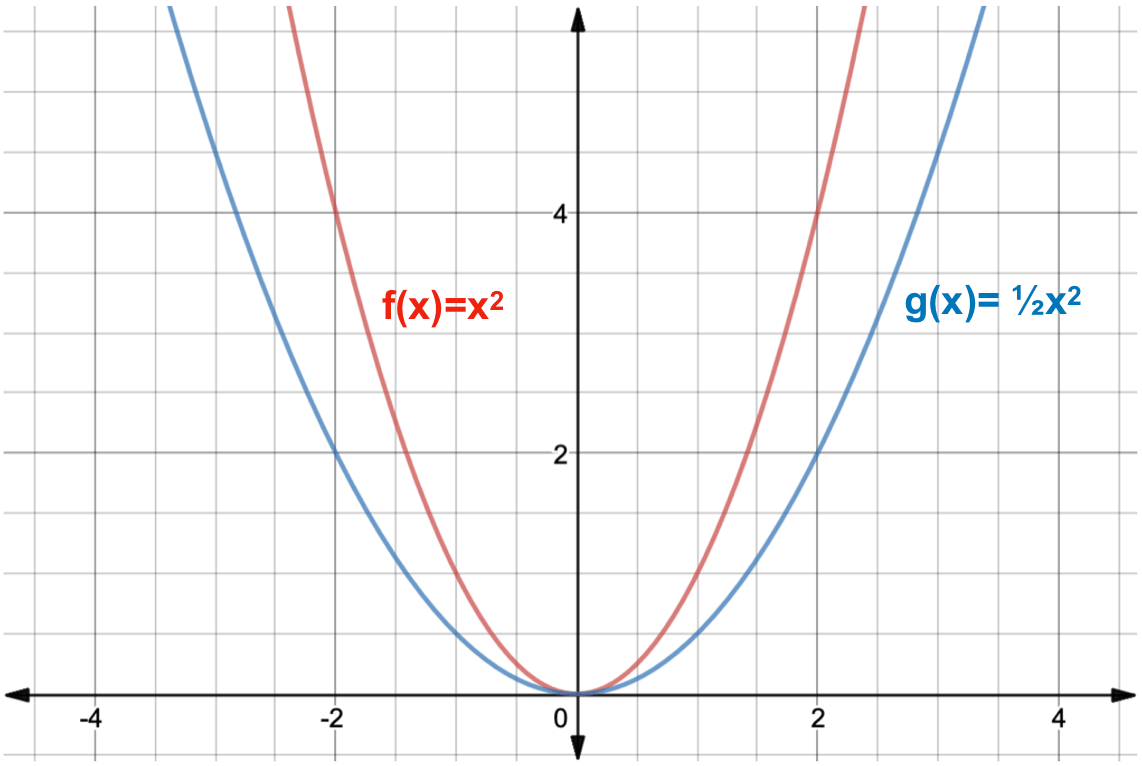


What Is A Function Transformation Expii



Graphing Square And Cube Root Functions Video Khan Academy
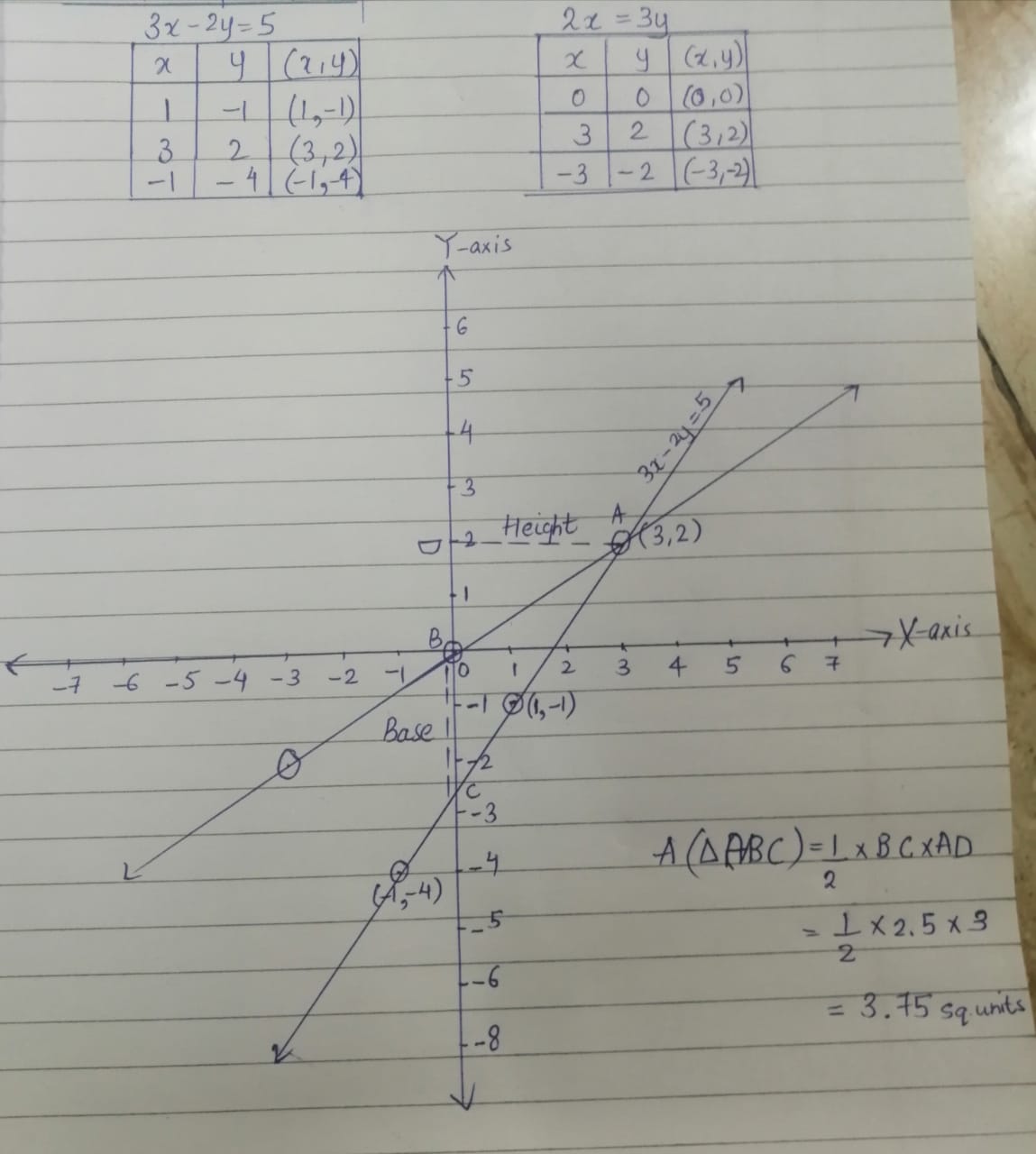


Use Graph Paper For This Question Draw The Graph Of 3x 2y 5 And 2x 3y On The Same Axes Use 2cm 1 Unit On Both The Axes And Plot Only 3
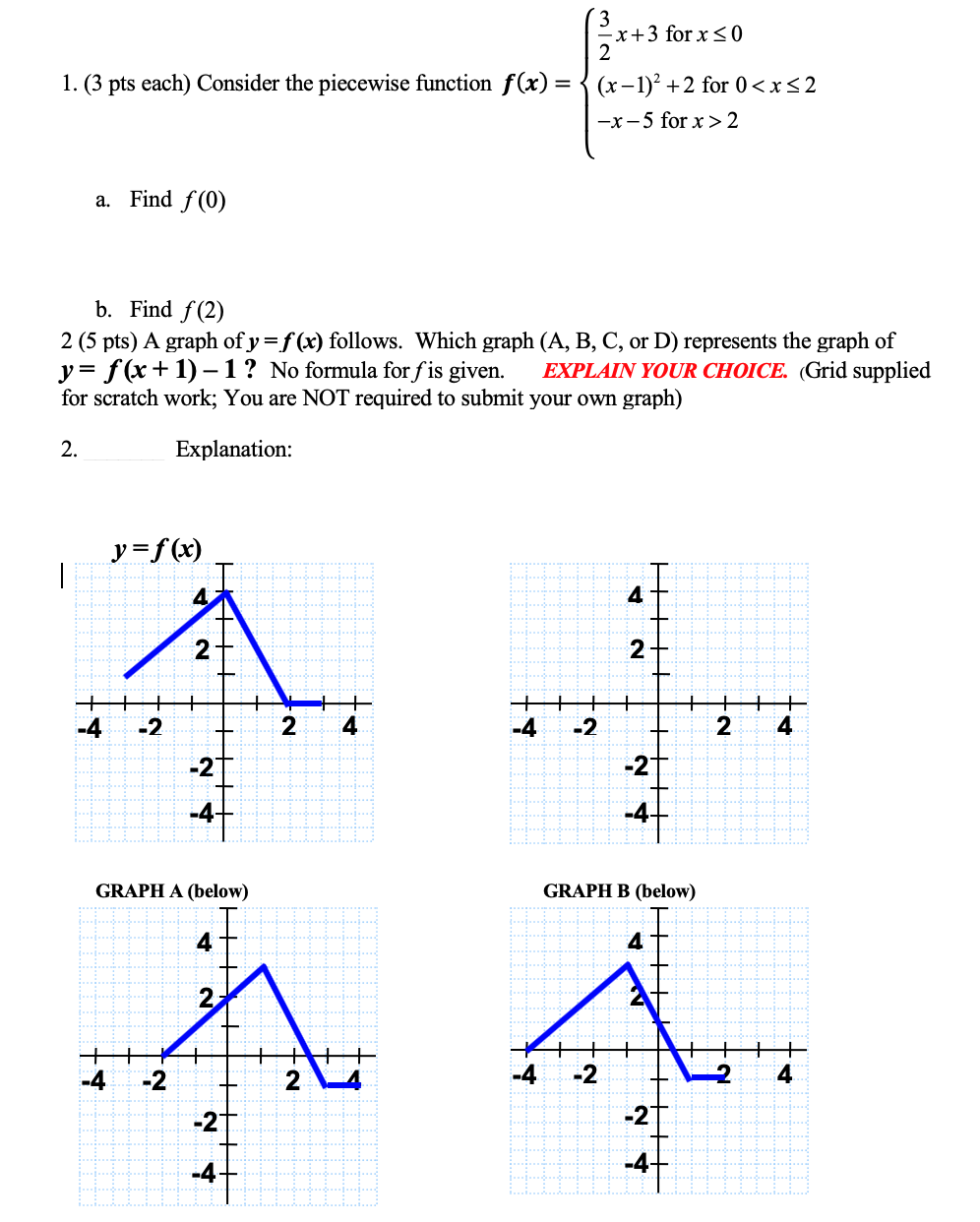


Solved X 3 For X 0 1 3 Pts Each Consider The Piecew Chegg Com



Rectangular Coordinate System



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



Ppt Warm Up Evaluate Each Expression For X 1 And Y 3 1 X 4 Y 2 2 X Y Powerpoint Presentation Id
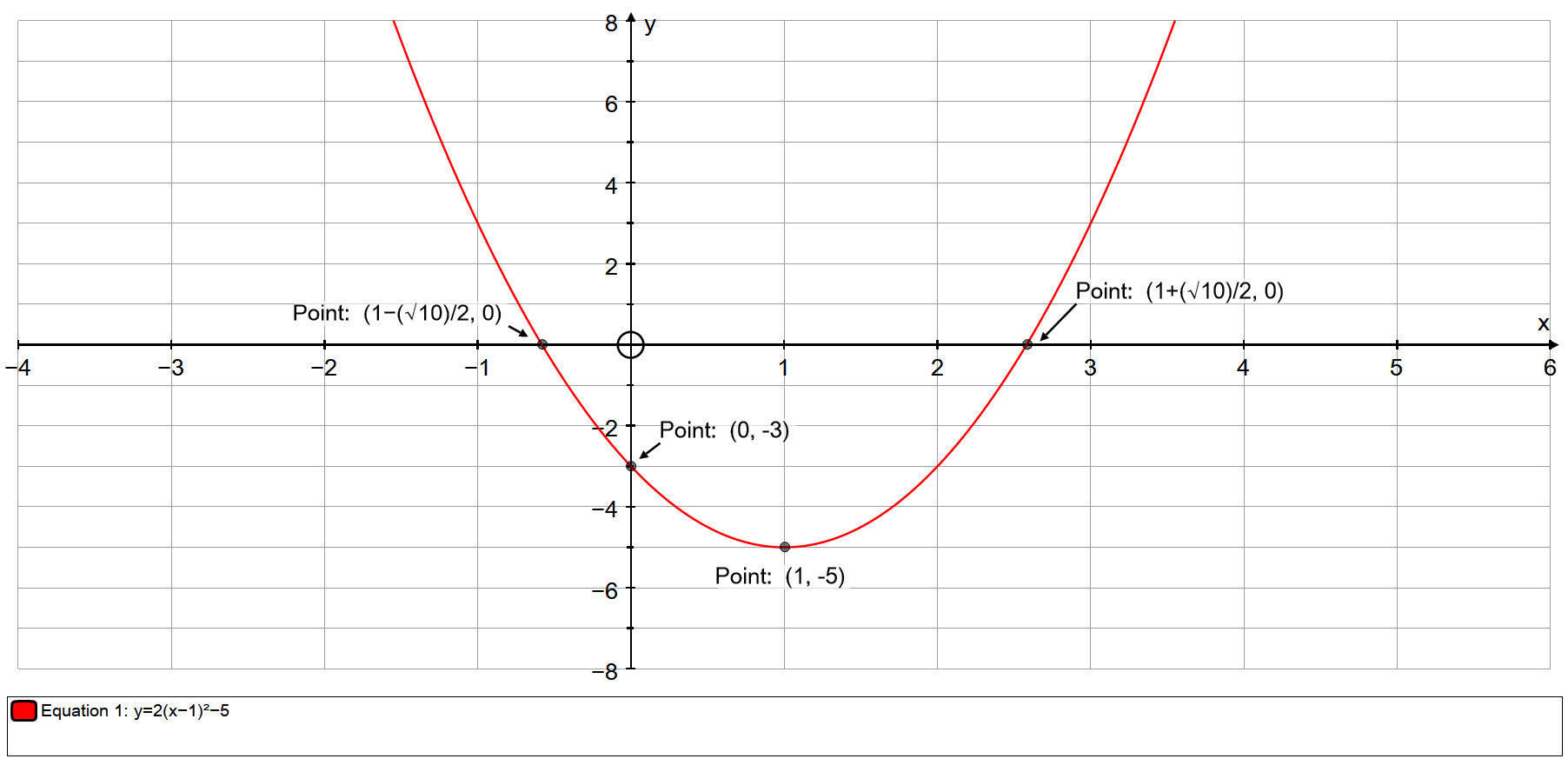


How Do You Graph The Parabola Y 2 X 1 2 5 Using Vertex Intercepts And Additional Points Socratic



2 Find The Translation That Transforms The Graph Y X 2
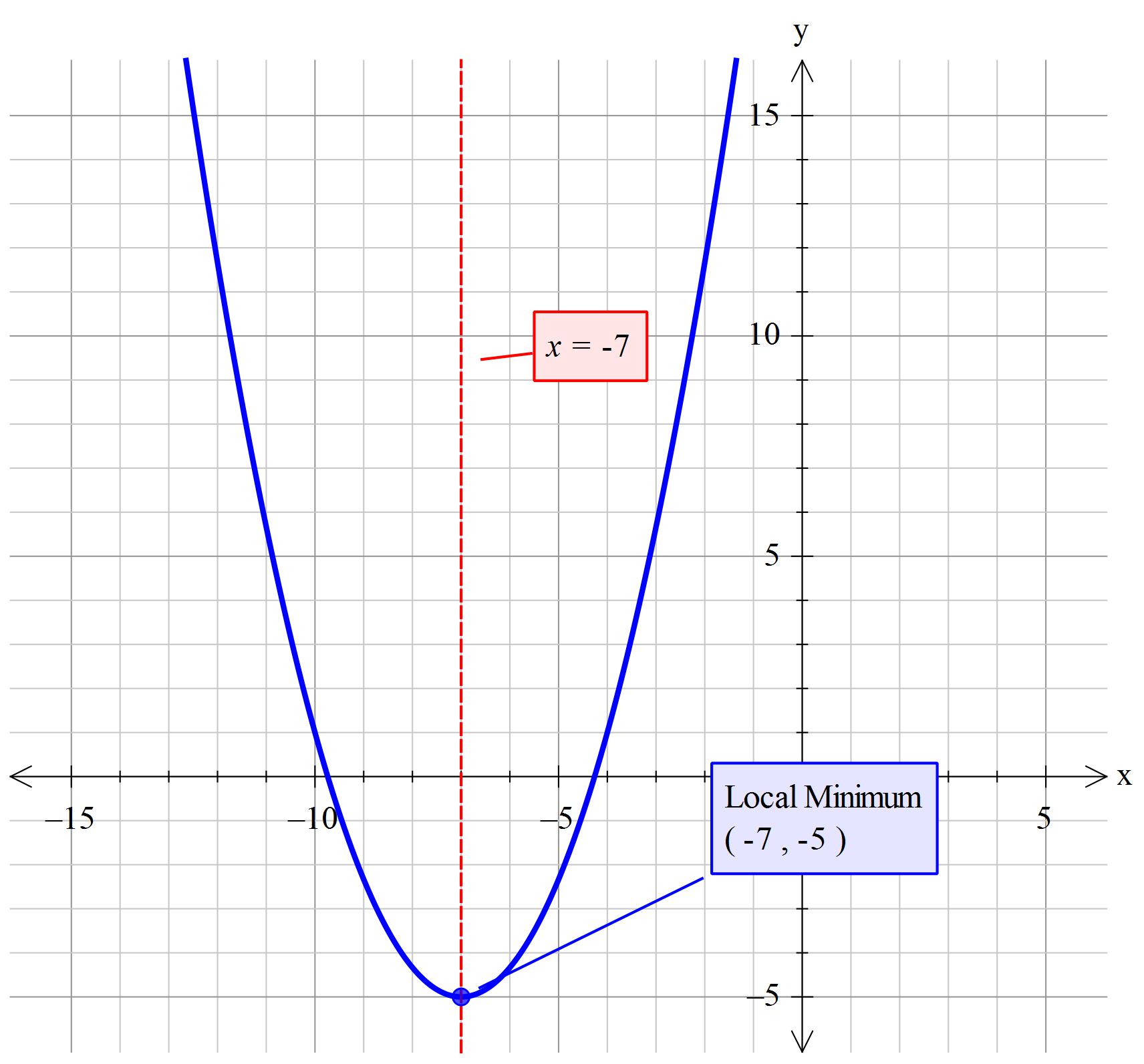


What Is The Axis Of Symmetry And Vertex For The Graph F X 2 3 X 7 2 5 Socratic



Draw The Graphs Of The Equations X 3 X 5 And 2x Y 4 0 Also Find The Area Of The Quadrilateral Youtube



1 Let F X 6x 7x Solution 2x 1 3x 2 X 1
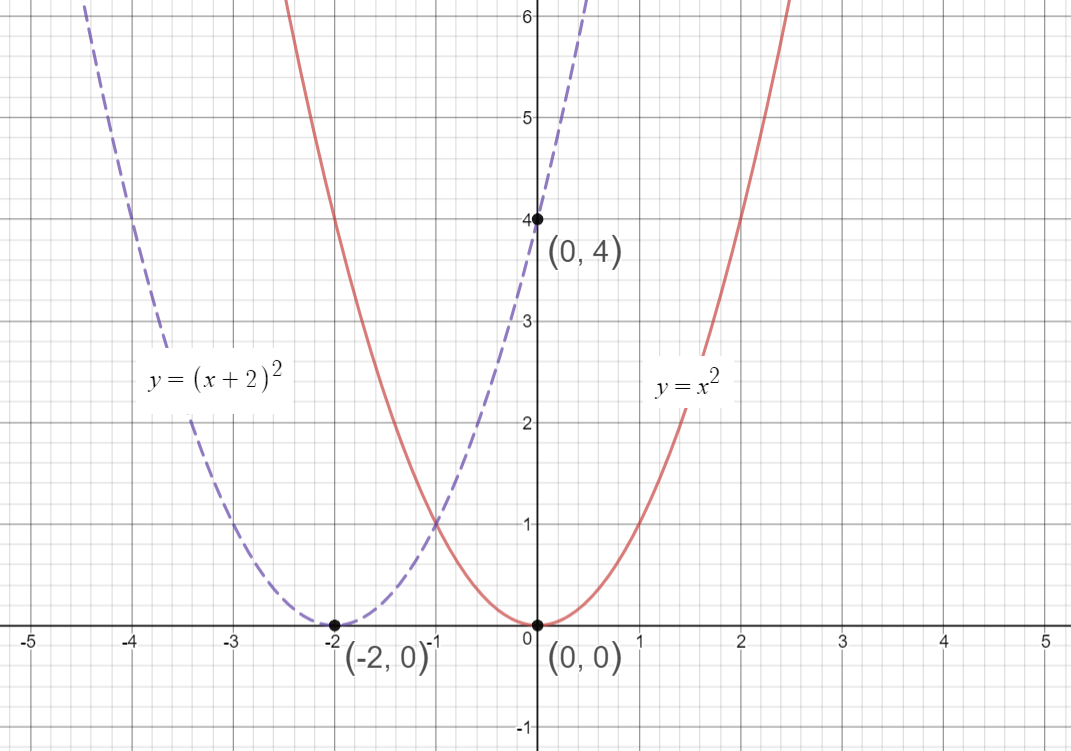


How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic
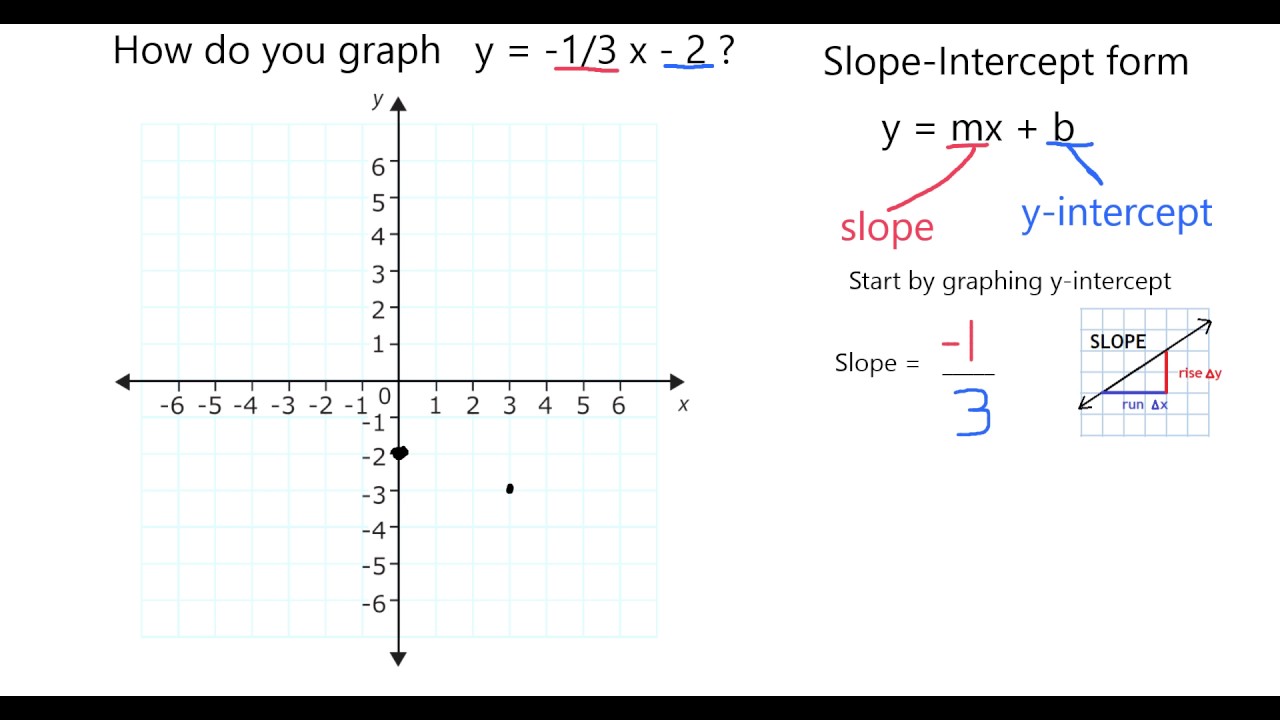


Graph In Slope Intercept Form Y 1 3 X 2 Youtube



Lesson 1 1 Pages 5 11 State The Domain And Range Of Each Relation Then State Whether The Relation Is A Function Write Yes Or No Pdf Free Download
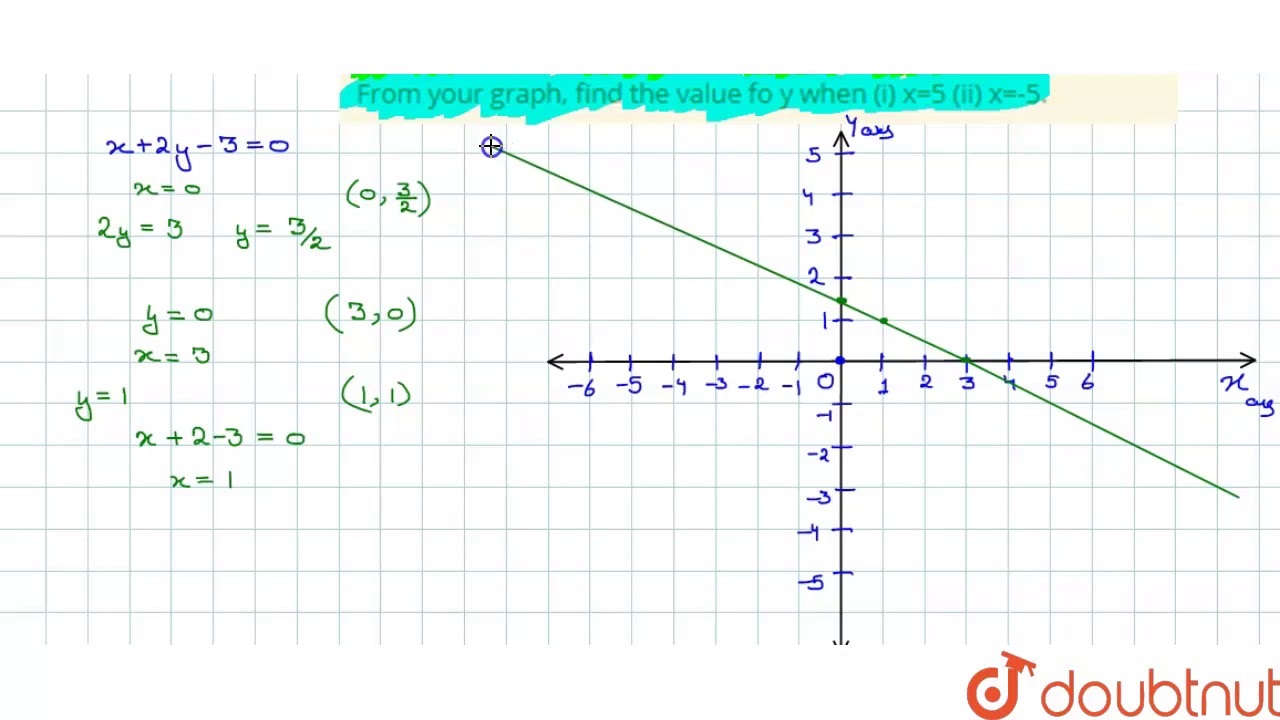


Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Fo Y When I X 5 I Youtube
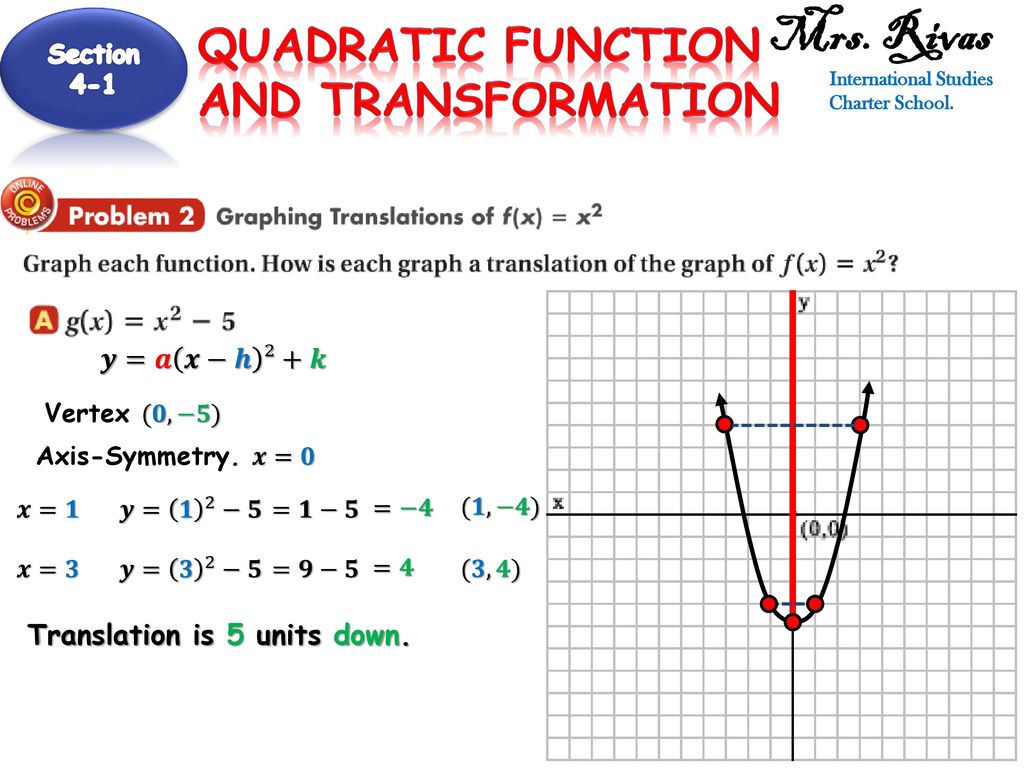


Mrs Rivas Ppt Download
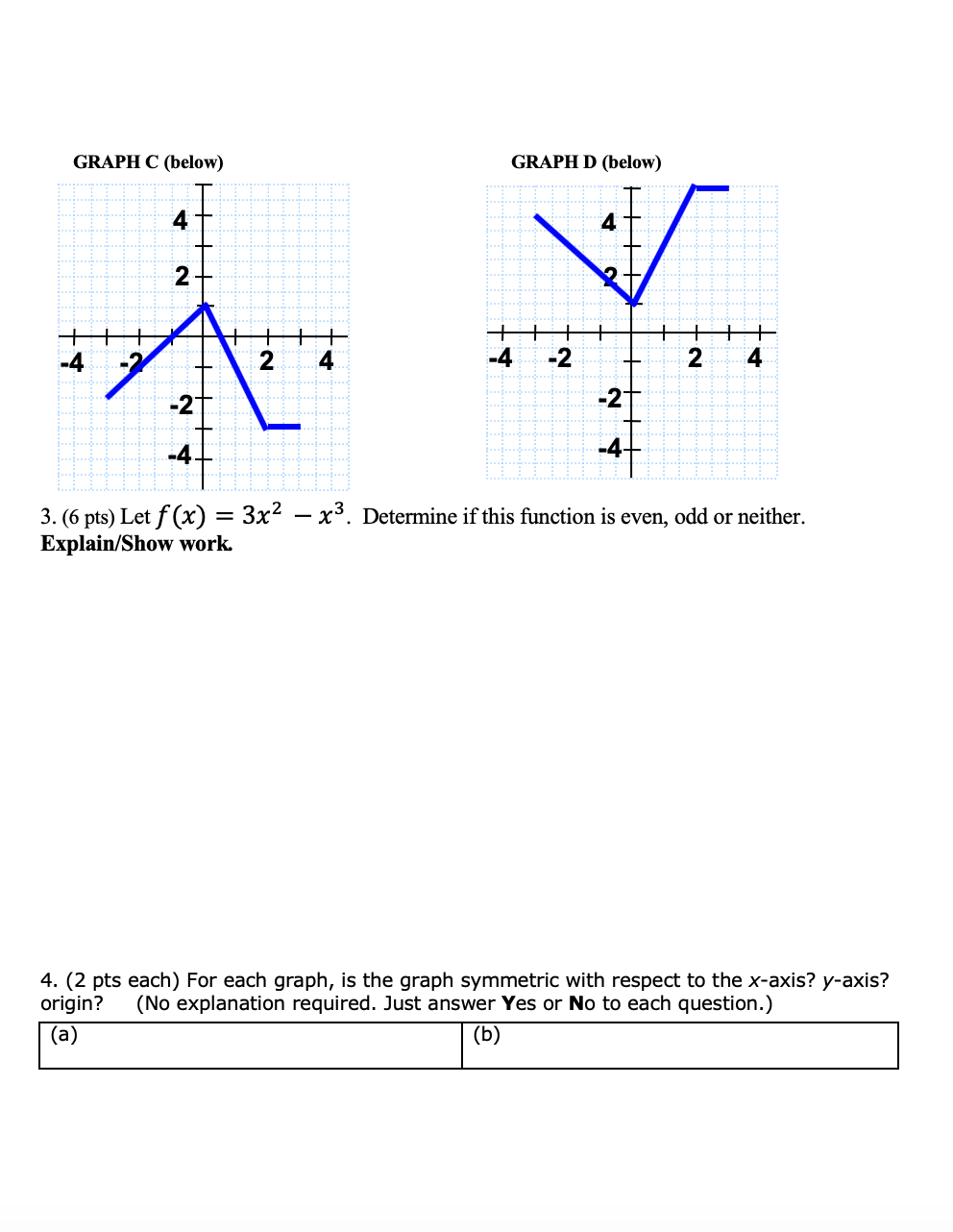


Solved X 3 For X 0 1 3 Pts Each Consider The Piecew Chegg Com



Graphing Parabolas



3 2 Graphs Of Functions Hunter College Math101
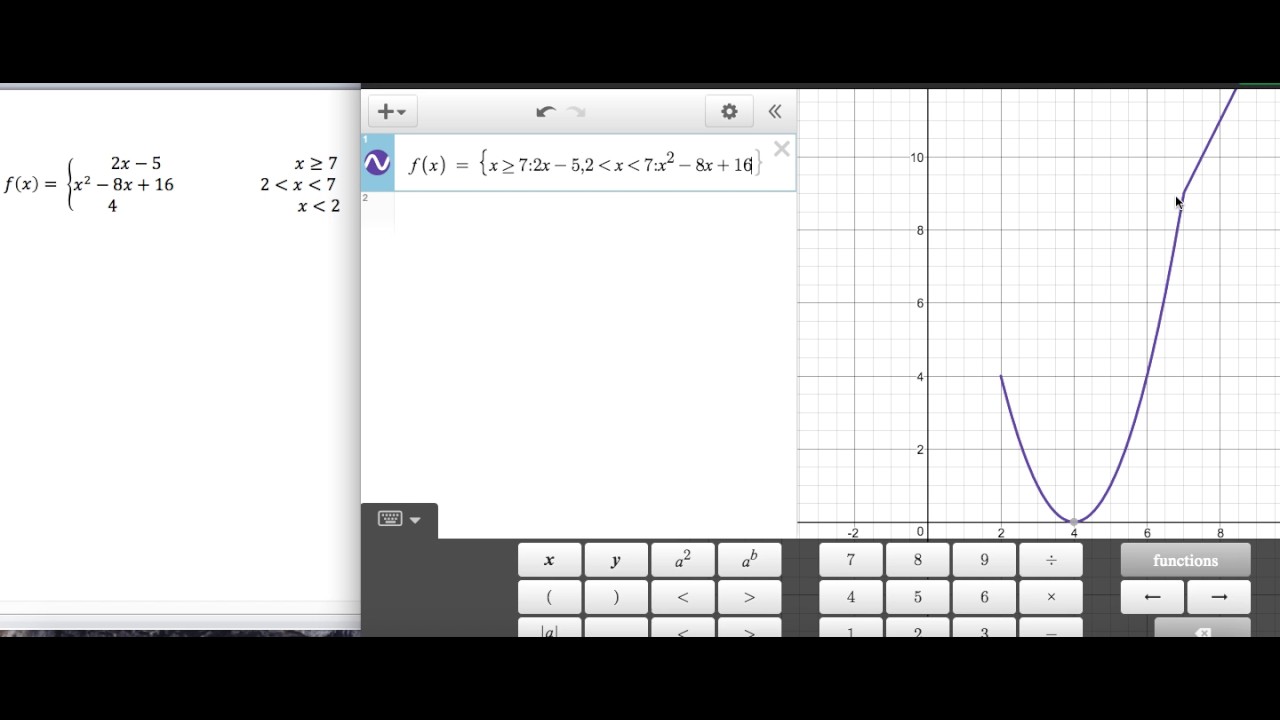


Piecewise Defined Functions College Algebra
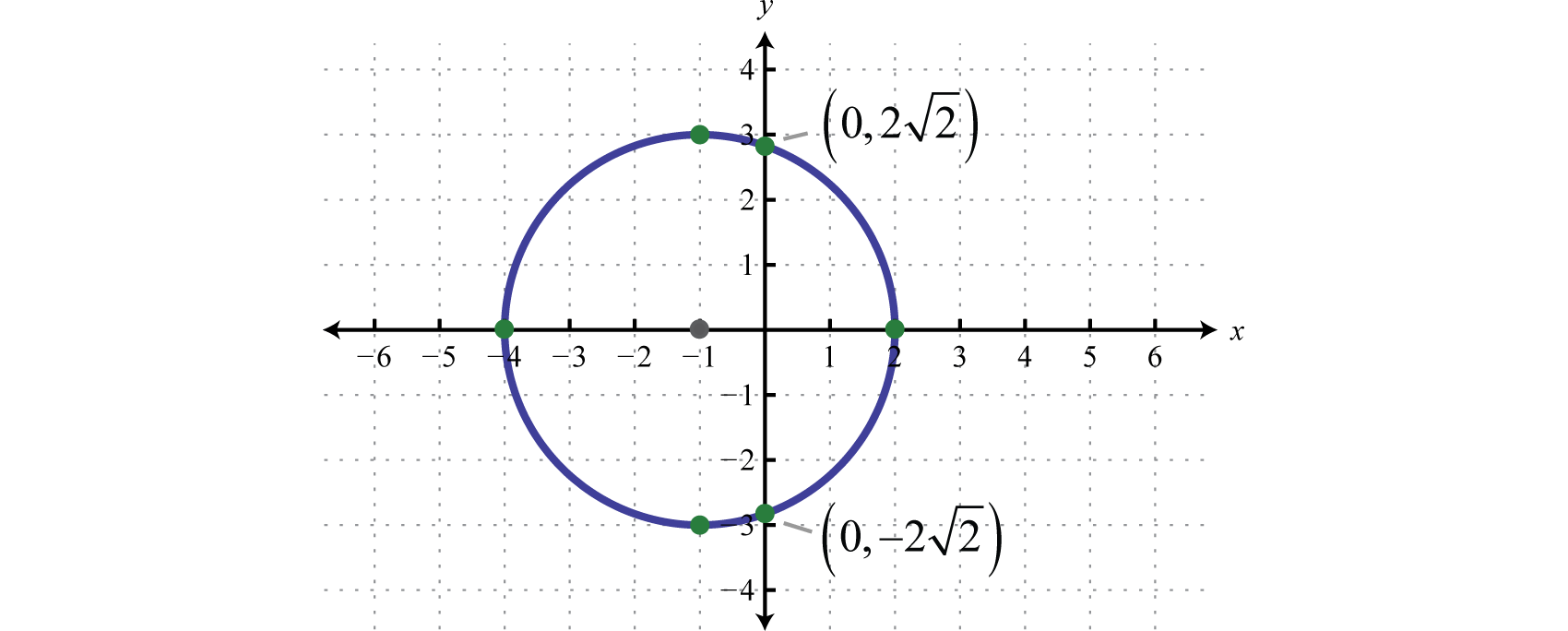


Circles
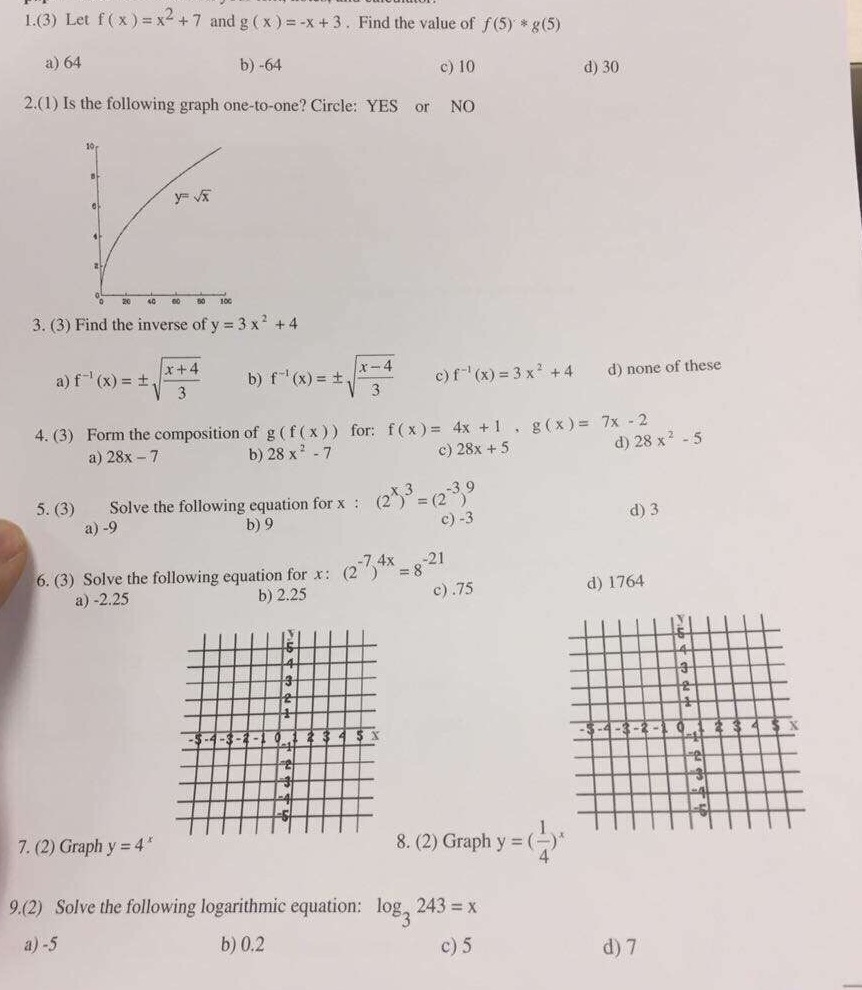


Solved 1 3 Let F X X2 7 And G X X 3 Find The Chegg Com
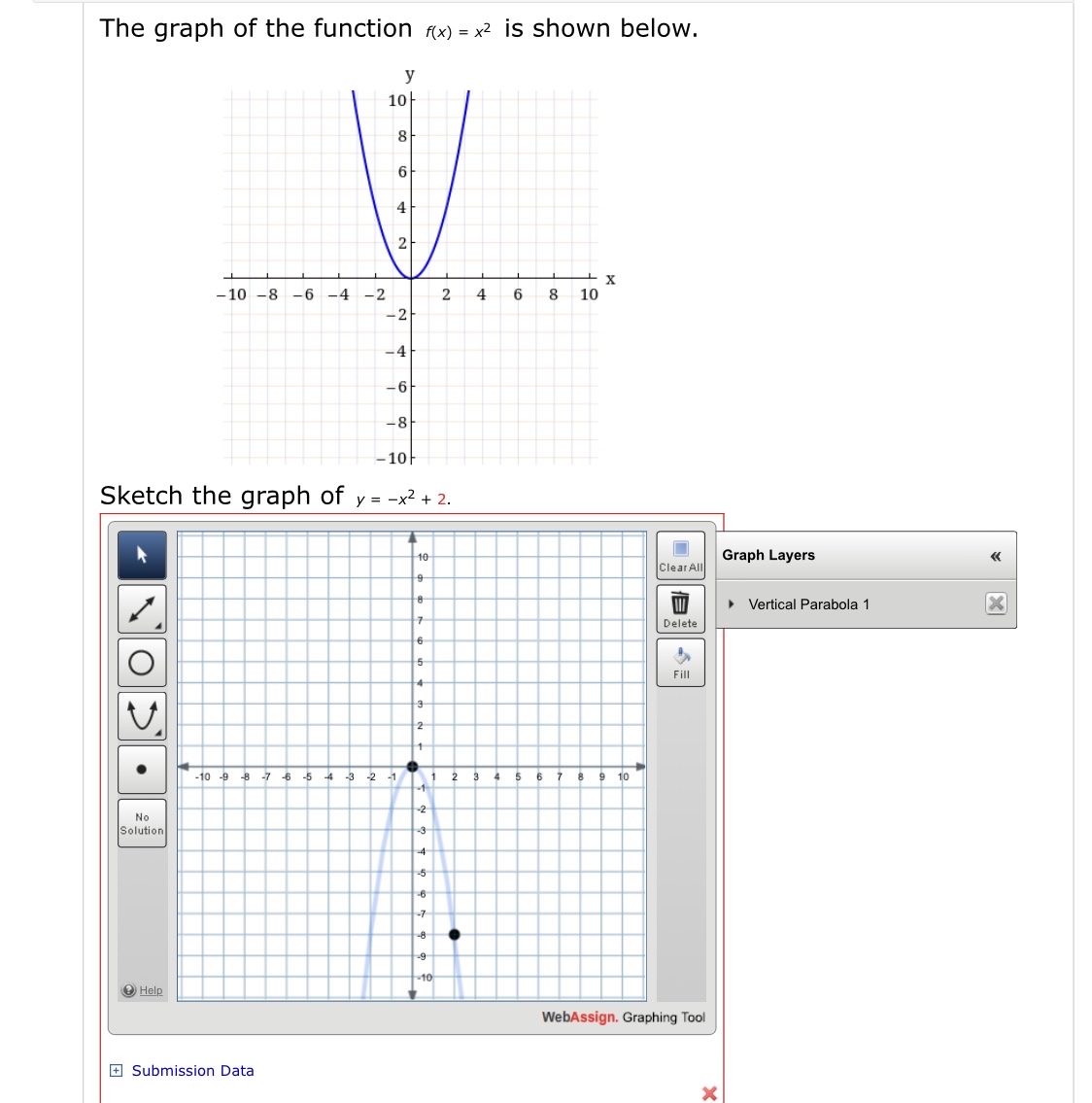


Answered The Graph Of The Function F X X2 Is Bartleby



Quadratic Functions
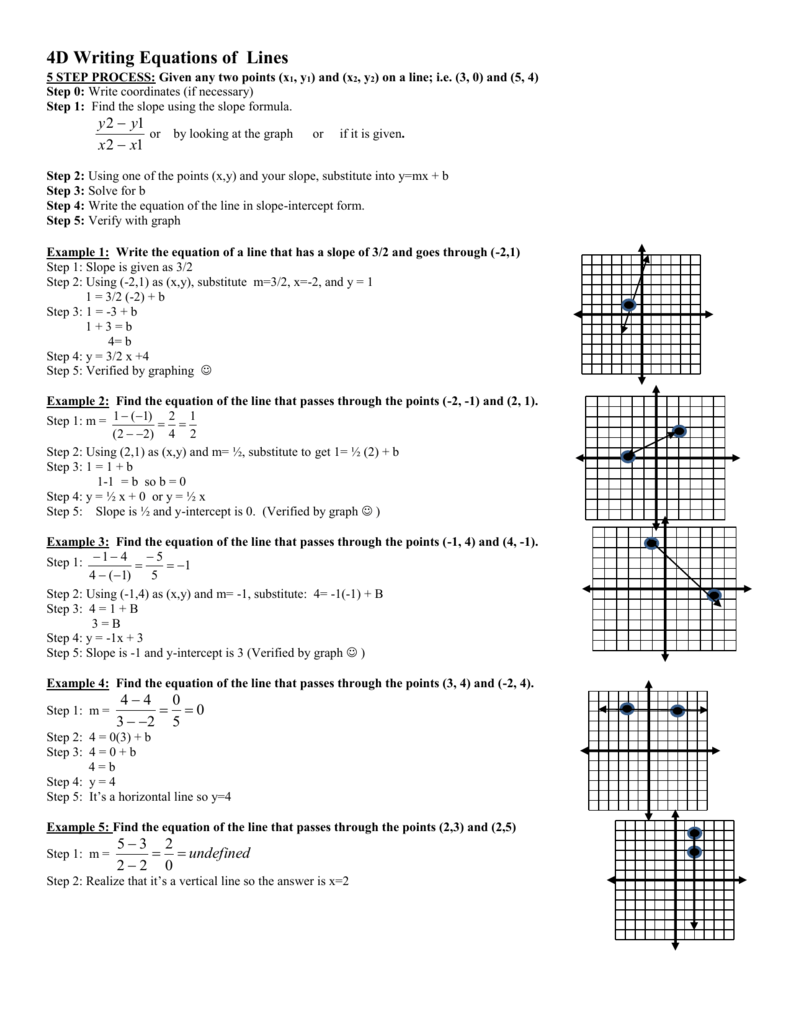


4d Writing Equations Of Lines



Answered Linear Equations 26 Chapter 1 Problems Bartleby
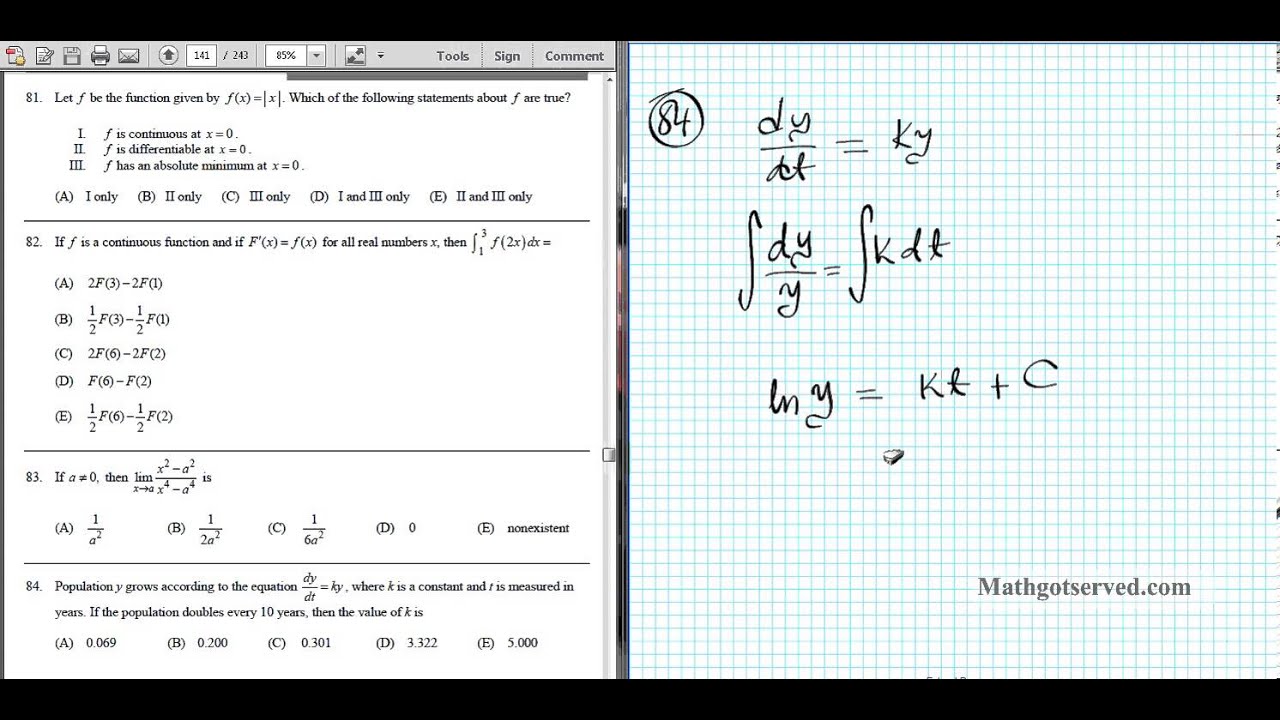


Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions



0 件のコメント:
コメントを投稿